构造二叉树系列

构造二叉树是一个常见的二叉树考点，相比于直接考察二叉树的遍历，这种题目的难度会更大。截止到目前(2020-02-08) LeetCode 关于构造二叉树一共有三道题目，分别是：

• 105. 从前序与中序遍历序列构造二叉树
• 106. 从中序与后序遍历序列构造二叉树
• 889. 根据前序和后序遍历构造二叉树

今天就让我们用一个套路一举攻破他们。

​

105. 从前序与中序遍历序列构造二叉树

题目描述

根据一棵树的前序遍历与中序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树：

    3
   / \
  9  20
    /  \
   15   7

思路

我们以题目给出的测试用例来讲解：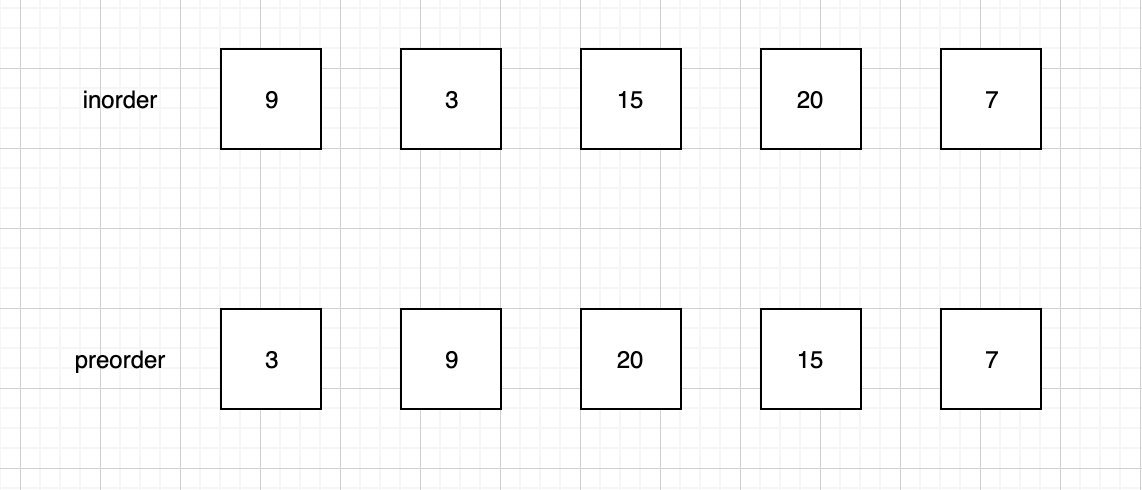

前序遍历是根左右，因此 preorder 第一个元素一定整个树的根。由于题目说明了没有重复元素，因此我们可以通过 val 去 inorder 找到根在 inorder 中的索引 i。
而由于中序遍历是左根右，我们容易找到 i 左边的都是左子树，i 右边都是右子树。

我使用红色表示根，蓝色表示左子树，绿色表示右子树。

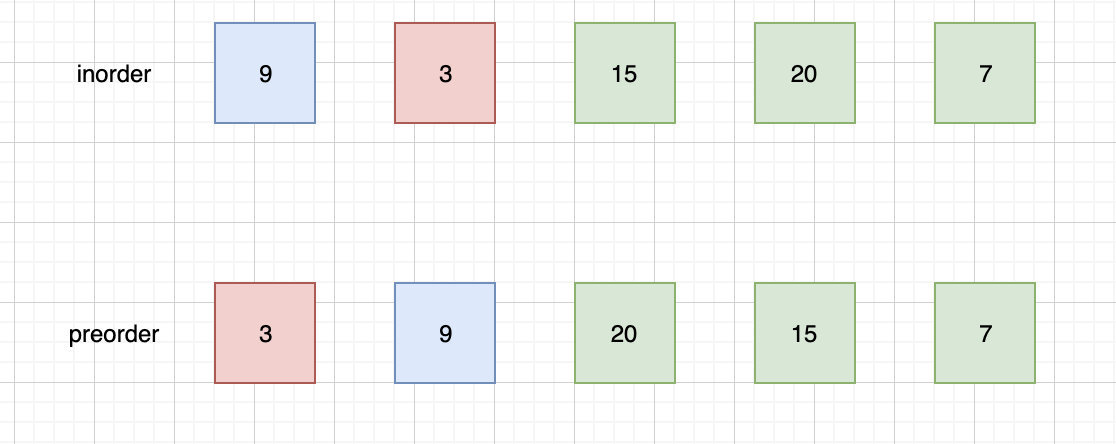
根据此时的信息，我们能构造的树是这样的：

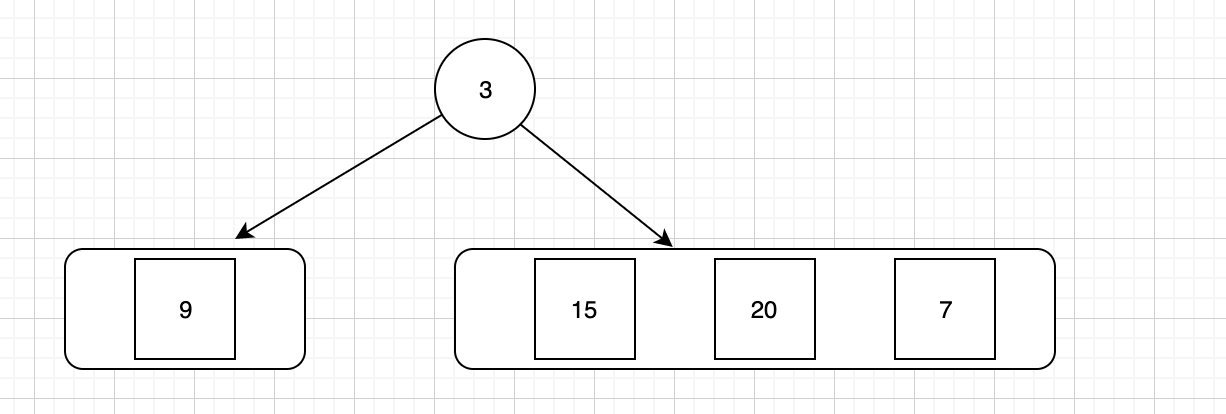
我们 preorder 继续向后移动一位，这个时候我们得到了第二个根节点”9“，实际上就是左子树的根节点。

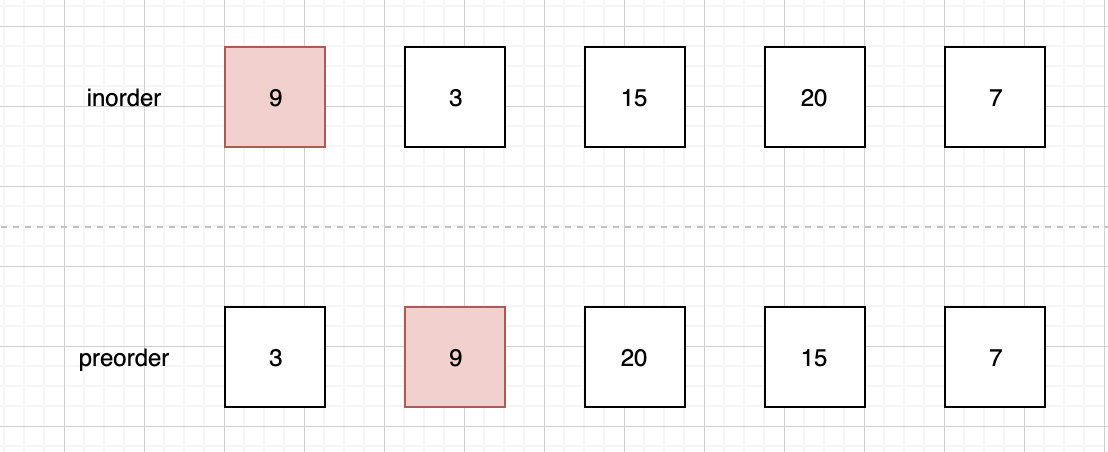
我们 preorder 继续向后移动一位，这个时候我们得到了第二个根节点”20“，实际上就是右子树的根节点。其中右子树由于个数大于 1，我们无法确定，我们继续执行上述逻辑。

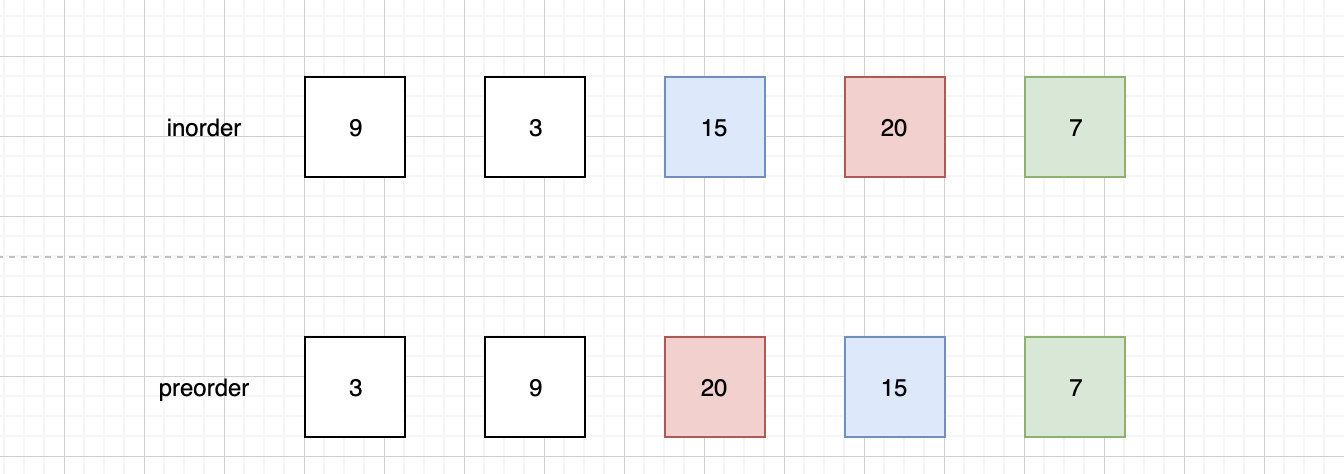
根据此时的信息，我们能构造的树是这样的：

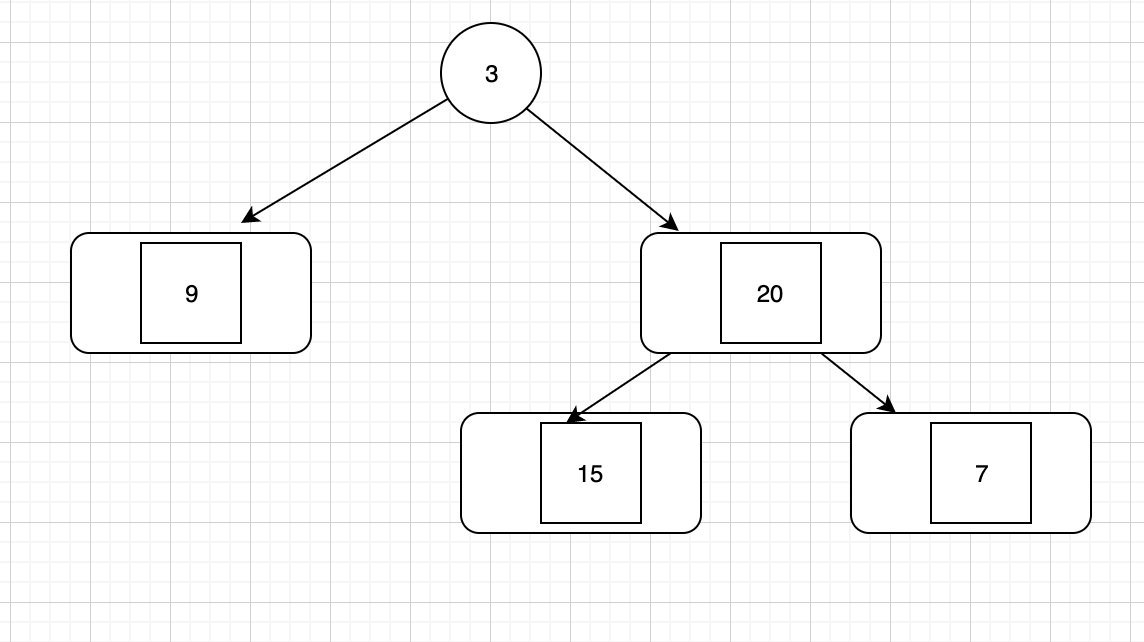
我们不断执行上述逻辑即可。简单起见，递归的时候每次我都开辟了新的数组，这个其实是没有必要的，我们可以通过四个变量来记录 inorder 和 preorder 的起始位置即可。

代码

代码支持：Python3

Python3 Code:

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        # 实际上inorder 和 postorder一定是同时为空的，因此你无论判断哪个都行
        if not preorder:
            return None
        root = TreeNode(preorder[0])

        i = inorder.index(root.val)
        root.left = self.buildTree(preorder[1:i + 1], inorder[:i])
        root.right = self.buildTree(preorder[i + 1:], inorder[i+1:])

        return root

复杂度分析

• 时间复杂度：由于每次递归我们的 inorder 和 preorder 的总数都会减 1，因此我们要递归 N 次，故时间复杂度为 $O(N)$，其中 N 为节点个数。
• 空间复杂度：我们使用了递归，也就是借助了额外的栈空间来完成， 由于栈的深度为 N，因此总的空间复杂度为 $O(N)$，其中 N 为节点个数。

空间复杂度忽略了开辟数组的内存消耗。

106. 从中序与后序遍历序列构造二叉树

如果你会了上面的题目，那么这个题目对你来说也不是难事，我们来看下。

题目描述

根据一棵树的中序遍历与后序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]
返回如下的二叉树：

    3
   / \
  9  20
    /  \
   15   7

思路

我们以题目给出的测试用例来讲解：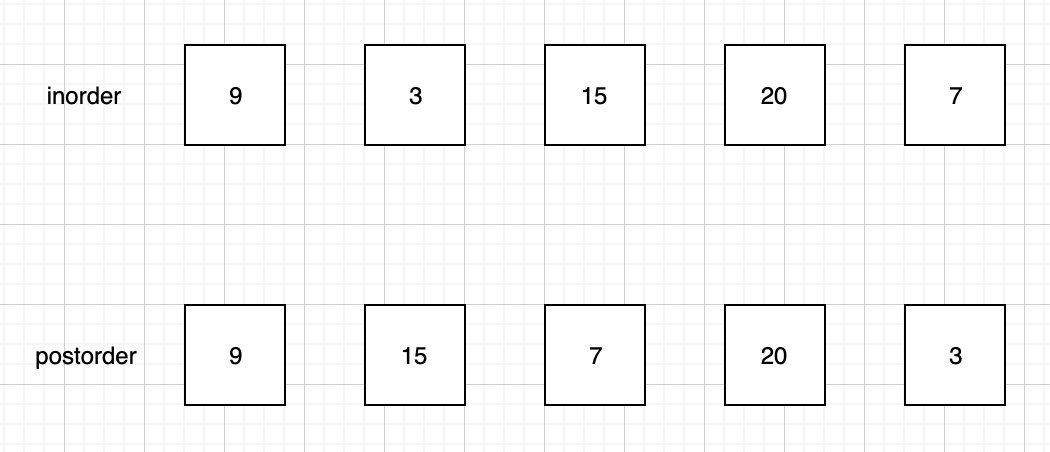

后序遍历是左右根，因此 postorder 最后一个元素一定整个树的根。由于题目说明了没有重复元素，因此我们可以通过 val 去 inorder 找到根在 inorder 中的索引 i。
而由于中序遍历是左根右，我们容易找到 i 左边的都是左子树，i 右边都是右子树。

我使用红色表示根，蓝色表示左子树，绿色表示右子树。

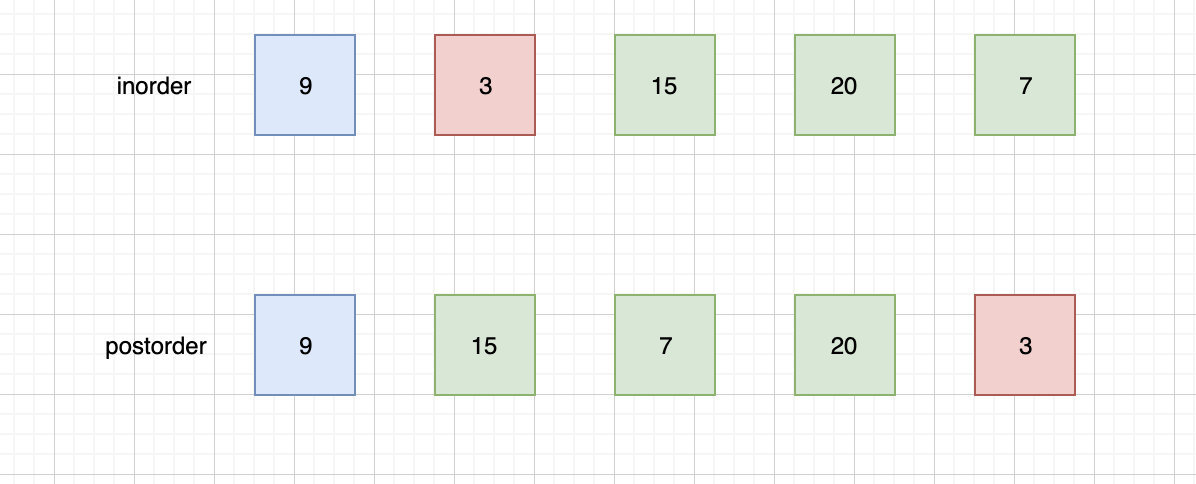
根据此时的信息，我们能构造的树是这样的：

其中右子树由于个数大于 1，我们无法确定，我们继续执行上述逻辑。我们 postorder 继续向前移动一位，这个时候我们得到了第二个根节点”20“，实际上就是右子树的根节点。

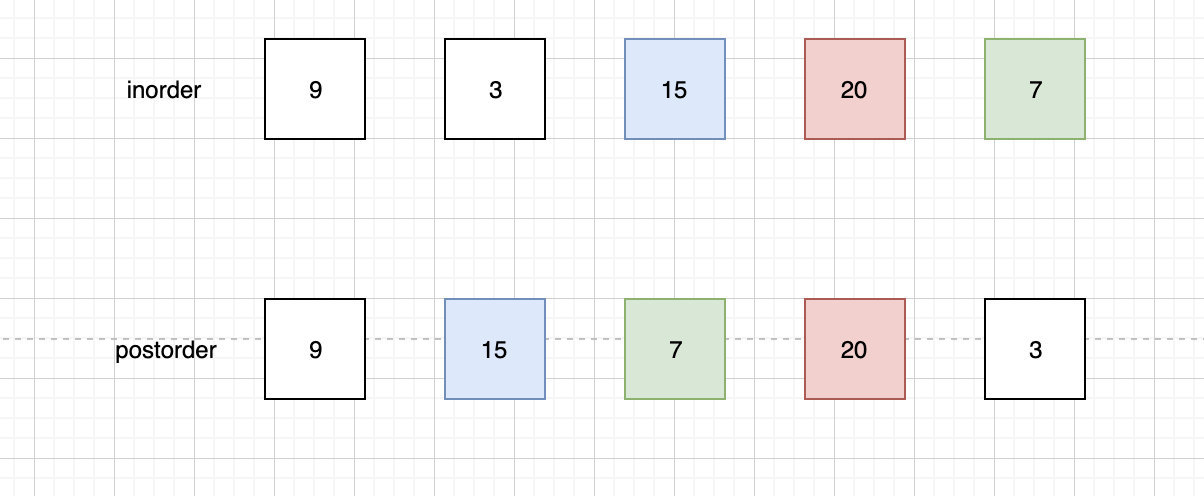
根据此时的信息，我们能构造的树是这样的：

我们不断执行上述逻辑即可。简单起见，递归的时候每次我都开辟了新的数组，这个其实是没有必要的，我们可以通过四个变量来记录 inorder 和 postorder 的起始位置即可。

代码

代码支持：Python3

Python3 Code:

class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
        # 实际上inorder 和 postorder一定是同时为空的，因此你无论判断哪个都行
        if not inorder:
            return None
        root = TreeNode(postorder[-1])
        i = inorder.index(root.val)
        root.left = self.buildTree(inorder[:i], postorder[:i])
        root.right = self.buildTree(inorder[i+1:], postorder[i:-1])

        return root

复杂度分析

• 时间复杂度：由于每次递归我们的 inorder 和 postorder 的总数都会减 1，因此我们要递归 N 次，故时间复杂度为 $O(N)$，其中 N 为节点个数。
• 空间复杂度：我们使用了递归，也就是借助了额外的栈空间来完成， 由于栈的深度为 N，因此总的空间复杂度为 $O(N)$，其中 N 为节点个数。

空间复杂度忽略了开辟数组的内存消耗。

889. 根据前序和后序遍历构造二叉树

题目描述

返回与给定的前序和后序遍历匹配的任何二叉树。

 pre 和 post 遍历中的值是不同的正整数。

 

示例：

输入：pre = [1,2,4,5,3,6,7], post = [4,5,2,6,7,3,1]
输出：[1,2,3,4,5,6,7]
 

提示：

1 <= pre.length == post.length <= 30
pre[] 和 post[] 都是 1, 2, ..., pre.length 的排列
每个输入保证至少有一个答案。如果有多个答案，可以返回其中一个。

思路

我们以题目给出的测试用例来讲解：

前序遍历是根左右，因此 preorder 第一个元素一定整个树的根，preorder 第二个元素（如果存在的话）一定是左子树。由于题目说明了没有重复元素，因此我们可以通过 val 去 postorder 找到 pre[1]在 postorder 中的索引 i。
而由于后序遍历是左右根，因此我们容易得出。 postorder 中的 0 到 i(包含)是左子树，preorder 的 1 到 i+1（包含）也是左子树。

其他部分可以参考上面两题。

代码

代码支持：Python3

Python3 Code:

class Solution:
    def constructFromPrePost(self, pre: List[int], post: List[int]) -> TreeNode:
        # 实际上pre 和 post一定是同时为空的，因此你无论判断哪个都行
        if not pre:
            return None
        node = TreeNode(pre[0])
        if len(pre) == 1:
            return node
        i = post.index(pre[1])

        node.left = self.constructFromPrePost(pre[1:i + 2], post[:i + 1])
        node.right = self.constructFromPrePost(pre[i + 2:], post[i + 1:-1])

        return node

复杂度分析

• 时间复杂度：由于每次递归我们的 postorder 和 preorder 的总数都会减 1，因此我们要递归 N 次，故时间复杂度为 $O(N)$，其中 N 为节点个数。
• 空间复杂度：我们使用了递归，也就是借助了额外的栈空间来完成， 由于栈的深度为 N，因此总的空间复杂度为 $O(N)$，其中 N 为节点个数。

空间复杂度忽略了开辟数组的内存消耗。

总结

如果你仔细对比一下的话，会发现我们的思路和代码几乎一模一样。注意到每次递归我们的两个数组个数都会减去 1，因此我们递归终止条件不难写出，并且递归问题规模如何缩小也很容易，那就是数组总长度减去 1。

我们拿最后一个题目来说：

node.left = self.constructFromPrePost(pre[1:i + 2], post[:i + 1])
node.right = self.constructFromPrePost(pre[i + 2:], post[i + 1:-1])

我们发现 pre 被拆分为两份，pre[1:i + 2]和 pre[i + 2:]。很明显总数少了 1，那就是 pre 的第一个元素。 也就是说如果你写出一个，其他一个不用思考也能写出来。

而对于 post 也一样，post[:i + 1] 和 post[i + 1:-1]，很明显总数少了 1，那就是 post 最后一个元素。

这个解题模板足够简洁，并且逻辑清晰，大家可以用我的模板试试～

简单起见，递归的时候每次我都开辟了新的数组，这个其实是没有必要的，我们可以通过四个变量来记录 inorder 和 postorder 的起始位置即可， 具体见下方代码区。

代码：

class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
        def dfs(inorder, i_start, i_end, postorder, p_start, p_end):
            if i_start > i_end: return None
            if i_start == i_end: return TreeNode(inorder[i_start])
            node = TreeNode(postorder[p_end])
            i = inorder.index(postorder[p_end])
            node.left = dfs(inorder, i_start, i - 1, postorder, p_start, p_start + (i - 1 - i_start))
            node.right = dfs(inorder, i + 1, i_end, postorder, p_start + (i - 1 - i_start) + 1, p_end - 1)
            return node
        return dfs(inorder, 0, len(inorder) - 1, postorder, 0, len(postorder) - 1)

updated:(有同学不懂为啥 post_end 是 post_start + i - 1 - in_start，我解释一下)

我上面提到了 实际上 inorder 的 长度和 postorder 长度是一样的。而：

• inorder 的长度是 i - 1 - in_start
• 因此 postorder 的长度也是 i - 1 - in_start
• postorder 的长度 = post_end - post_start
• 因此 post_end 就是 post_start + i - 1 - in_start

复杂度分析

• 时间复杂度：由于每次递归我们的 inorder 和 postorder 的总数都会减 1，因此我们要递归 N 次，故时间复杂度为 $O(N)$，其中 N 为节点个数。
• 空间复杂度：我们使用了递归，也就是借助了额外的栈空间来完成， 由于栈的深度为 N，因此总的空间复杂度为 $O(N)$，其中 N 为节点个数。

关注我

更多题解可以访问我的 LeetCode 题解仓库：https://github.com/azl397985856/leetcode 。 目前已经 30K star 啦。

大家也可以关注我的公众号《力扣加加》获取更多更新鲜的 LeetCode 题解