关于并查集的题目不少,官方给的数据是 30 道(截止 2020-02-20),但是有一些题目虽然官方没有贴并查集标签,但是使用并查集来说确非常简单。这类题目如果掌握模板,那么刷这种题会非常快,并且犯错的概率会大大降低,这就是模板的好处。
我这里总结了几道并查集的题目:
大家可以学了模板之后去套用一下上面的三道题,做不出来的可以看看我的题解。
并查集概述
并查集算法,主要是解决图论中「动态连通性」问题的
Union-Find 算法解决的是图的动态连通性问题,这个算法本身不难,能不能应用出来主要是看你抽象问题的能力,是否能够把原始问题抽象成一个有关图论的问题。
如果你对这个算法不是很明白,推荐看一下这篇文章Union-Find 算法详解,讲的非常详细。
你可以把并查集的元素看成部门的人,几个人可以组成一个部门个数。
并查集核心的三个方法分别是union, find, connected。
union: 将两个人所在的两个部门合并成一个部门(如果两个人是相同部门,实际山不需要合并)
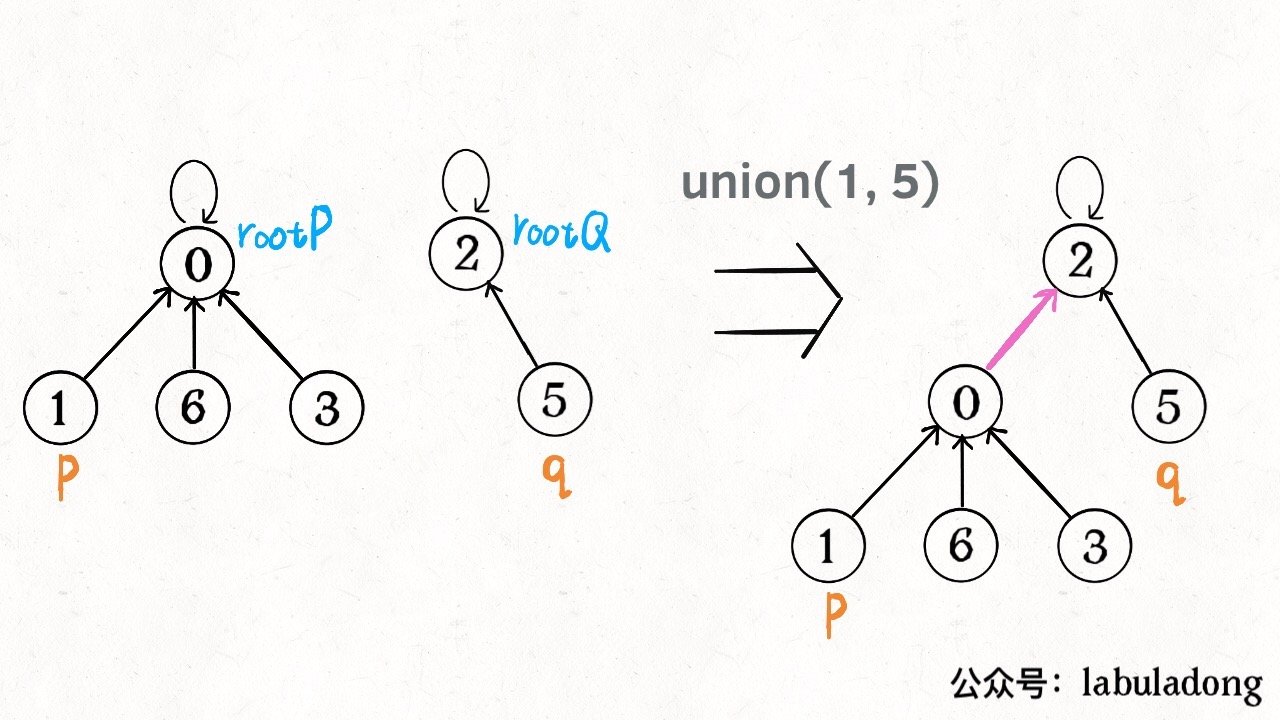
(图来自 labuladong)
find: 查找某个人的部门 leaderconnnected: 判断两个人是否是一个部门的
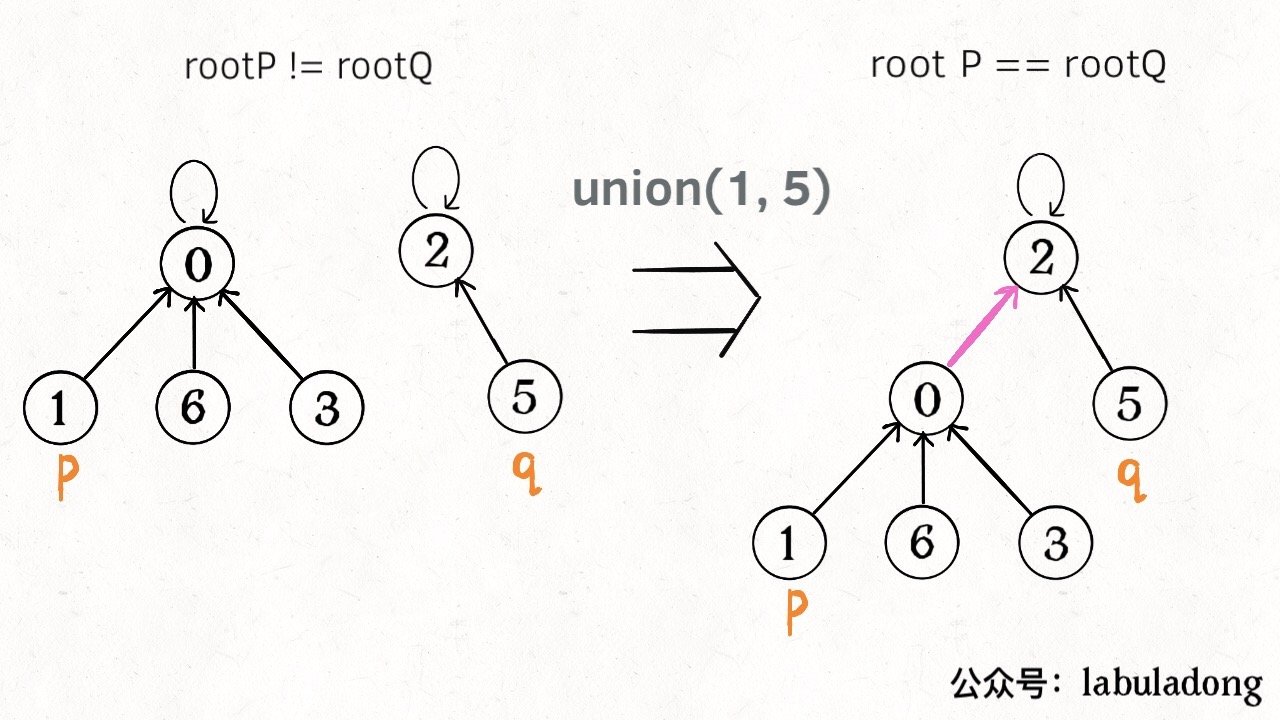
(图来自 labuladong)
模板
这是一个我经常使用的模板,我会根据具体题目做细小的变化,但是大体是不变的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| class UF:
parent = {}
cnt = 0
def __init__(self, M):
def find(self, x):
while x != self.parent[x]:
x = self.parent[x]
return x
def union(self, p, q):
if self.connected(p, q): return
self.parent[self.find(p)] = self.find(q)
self.cnt -= 1
def connected(self, p, q):
return self.find(p) == self.find(q)
|
如果你想要更好的性能,这个模板更适合你,相应地代码稍微有一点复杂。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class UF:
parent = {}
size = {}
cnt = 0
def __init__(self, M):
def find(self, x):
while x != self.parent[x]:
x = self.parent[x]
self.parent[x] = self.parent[self.parent[x]];
return x
def union(self, p, q):
if self.connected(p, q): return
leader_p = self.find(p)
leader_q = self.find(q)
if self.size[leader_p] < self.size[leader_q]:
self.parent[leader_p] = leader_q
else:
self.parent[leader_q] = leader_p
self.cnt -= 1
def connected(self, p, q):
return self.find(p) == self.find(q)
|
大家可以根据情况使用不同的模板。





