【LeetCode 日记】 84. 柱状图中最大的矩形

这是一道 Hard 难度的题目，本题的解法很多，让我们来看一下。

​

原题地址： https://leetcode-cn.com/problems/largest-rectangle-in-histogram/

题目描述

`
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

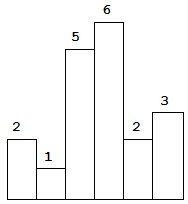
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

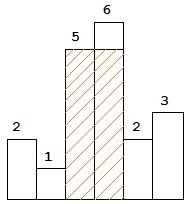
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例：

输入：[2,1,5,6,2,3]
输出：10

暴力枚举 - 左右端点法（TLE）

思路

我们暴力尝试所有可能的矩形。由于矩阵是二维图形， 我我们可以使用左右两个端点来唯一确认一个矩阵。因此我们使用双层循环枚举所有的可能性即可。 而矩形的面积等于（右端点坐标 - 左端点坐标 + 1) * 最小的高度，最小的高度我们可以在遍历的时候顺便求出。

代码

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        n, ans = len(heights), 0
        if n != 0:
            ans = heights[0]
        for i in range(n):
            height = heights[i]
            for j in range(i, n):
                height = min(height, heights[j])
                ans = max(ans, (j - i + 1) * height)
        return ans

复杂度分析

• 时间复杂度：$O(N^2)$
• 空间复杂度：$O(1)$

暴力枚举 - 中心扩展法（TLE）

思路

我们仍然暴力尝试所有可能的矩形。只不过我们这一次从中心向两边进行扩展。对于每一个 i，我们计算出其左边第一个高度小于它的索引 p，同样地，计算出右边第一个高度小于它的索引 q。那么以 i 为最低点能够构成的面积就是(q - p - 1) * heights[i]。 这种算法毫无疑问也是正确的。 我们证明一下，假设 f(i) 表示求以 i 为最低点的情况下，所能形成的最大矩阵面积。那么原问题转化为max(f(0), f(1), f(2), ..., f(n - 1))。

具体算法如下：

• 我们使用 l 和 r 数组。l[i] 表示 左边第一个高度小于它的索引，r[i] 表示 右边第一个高度小于它的索引。
• 我们从前往后求出 l，再从后往前计算出 r。
• 再次遍历求出所有的可能面积，并取出最大的。

代码

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        n = len(heights)
        l, r, ans = [-1] * n, [n] * n, 0
        for i in range(1, n):
            j = i - 1
            while j >= 0 and heights[j] >= heights[i]:
                j -= 1
            l[i] = j
        for i in range(n - 2, -1, -1):
            j = i + 1
            while j < n and heights[j] >= heights[i]:
                j += 1
            r[i] = j
        for i in range(n):
            ans = max(ans, heights[i] * (r[i] - l[i] - 1))
        return ans

复杂度分析

• 时间复杂度：$O(N^2)$
• 空间复杂度：$O(N)$

优化中心扩展法（Accepted）

思路

实际上我们内层循环没必要一步一步移动，我们可以直接将j -= 1 改成 j = l[j], j += 1 改成 j = r[j]。

代码

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        n = len(heights)
        l, r, ans = [-1] * n, [n] * n, 0

        for i in range(1, n):
            j = i - 1
            while j >= 0 and heights[j] >= heights[i]:
                j = l[j]
            l[i] = j
        for i in range(n - 2, -1, -1):
            j = i + 1
            while j < n and heights[j] >= heights[i]:
                j = r[j]
            r[i] = j
        for i in range(n):
            ans = max(ans, heights[i] * (r[i] - l[i] - 1))
        return ans

复杂度分析

• 时间复杂度：$O(N)$
• 空间复杂度：$O(N)$

单调栈（Accepted）

思路

实际上，读完第二种方法的时候，你应该注意到了。我们的核心是求左边第一个比 i 小的和右边第一个比 i 小的。 如果你熟悉单调栈的话，那么应该会想到这是非常适合使用单调栈来处理的场景。

为了简单起见，我在 heights 首尾添加了两个哨兵元素，这样可以减少边界处理的额外代码。

代码

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        n, heights, st, ans = len(heights), [0] + heights + [0], [], 0
        for i in range(n + 2):
            while st and heights[st[-1]] > heights[i]:
                ans = max(ans, heights[st.pop(-1)] * (i - st[-1] - 1))
            st.append(i)
        return ans

复杂度分析

• 时间复杂度：$O(N)$
• 空间复杂度：$O(N)$

欢迎关注我的公众号《脑洞前端》获取更多更新鲜的 LeetCode 题解