【LeetCode日记】 101. 对称二叉树

​

题目地址(101. 对称二叉树)

https://leetcode-cn.com/problems/symmetric-tree/

题目描述

给定一个二叉树，检查它是否是镜像对称的。

 

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

    1
   / \
  2   2
 / \ / \
3  4 4  3
 

但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:

    1
   / \
  2   2
   \   \
   3    3
 

进阶：

你可以运用递归和迭代两种方法解决这个问题吗？

思路

看到这题的时候，我的第一直觉是 DFS。然后我就想:如果左子树是镜像，并且右子树也是镜像，是不是就说明整体是镜像？。经过几秒的思考， 这显然是不对的，不符合题意。

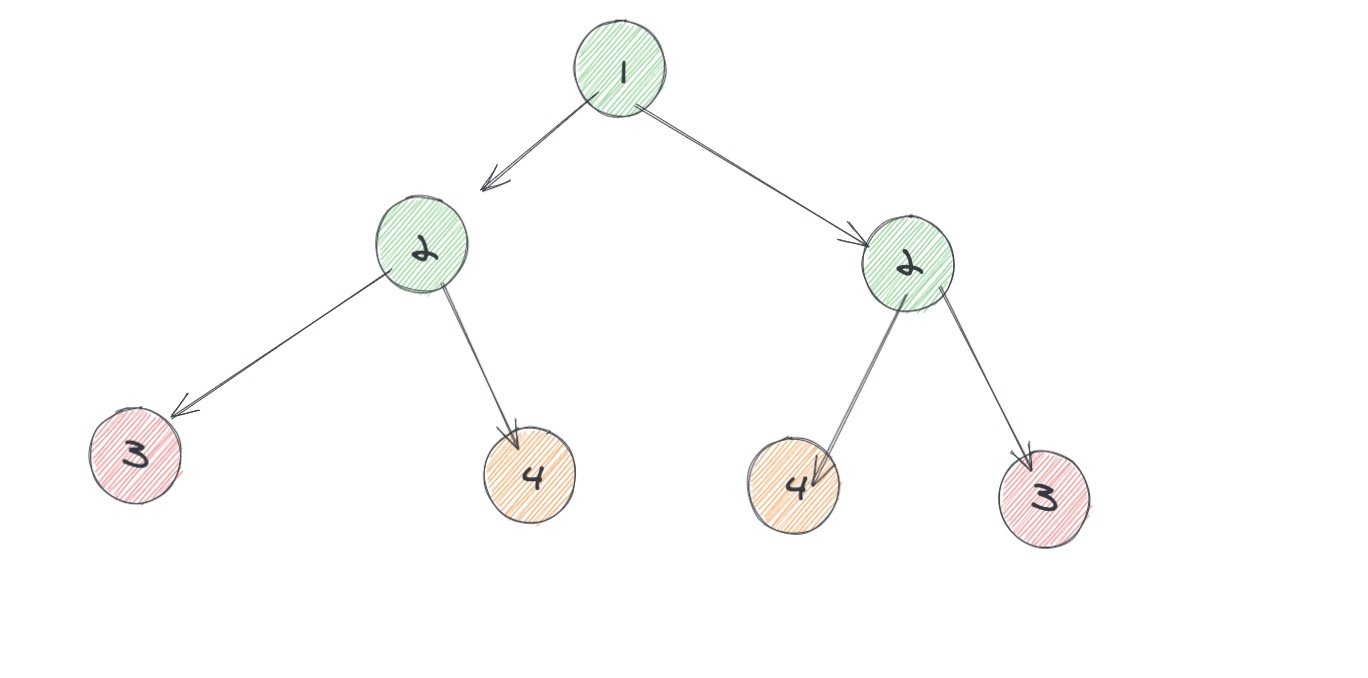
很明显其中左子树中的节点会和右子树中的节点进行比较，我把比较的元素进行了颜色区分，方便大家看。

这里我的想法是：遍历每一个节点的时候，我都可以通过某种方法知道它对应的对称节点是谁。这样的话我直接比较两者是否一致就行了。

最初我的想法是两次遍历，第一次遍历的同时将遍历结果存储到哈希表中，然后第二次遍历去哈希表取。

这种方法可行，但是需要 N 的空间（N 为节点总数）。我想到如果两者可以同时进行遍历，是不是就省去了哈希表的开销。

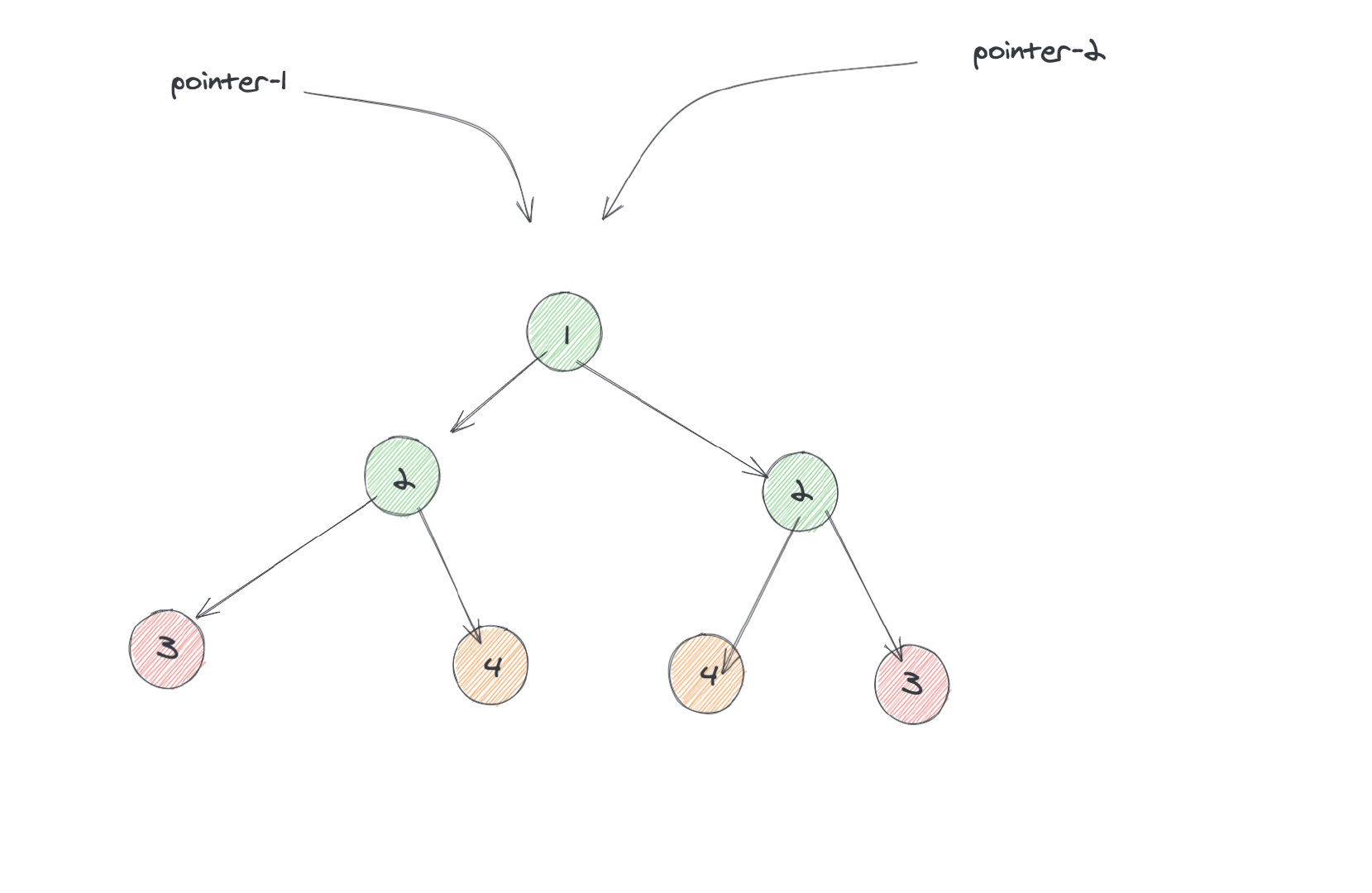
如果不明白的话，我举个简单例子：

给定一个数组，检查它是否是镜像对称的。例如，数组 [1,2,2,3,2,2,1] 是对称的。

如果用哈希表的话大概是：

seen = dict()
for i, num in enumerate(nums):
    seen[i] = num
for i, num in enumerate(nums):
    if  seen[len(nums) - 1 - i] != num:
      return False
return True

而同时遍历的话大概是这样的：

l = 0
r = len(nums) - 1

while l < r:
   if nums[l] != nums[r]: return False
   l += 1
   r -= 1
return True

其实更像本题一点的话应该是从中间分别向两边扩展 😂

代码

class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        def dfs(root1, root2):
            if root1 == root2: return True
            if not root1 or not root2: return False
            if root1.val != root2.val: return False
            return dfs(root1.left, root2.right) and dfs(root1.right, root2.left)
        if not root: return True
        return dfs(root.left, root.right)

_复杂度分析_

• 时间复杂度：$O(N)$，其中 N 为节点数。
• 空间复杂度：递归的深度最高为节点数，因此空间复杂度是 $O(N)$，其中 N 为节点数。

更多题解可以访问我的 LeetCode 题解仓库：https://github.com/azl397985856/leetcode 。 目前已经 30K star 啦。

大家也可以关注我的公众号《脑洞前端》获取更多更新鲜的 LeetCode 题解