【LeetCode日记】 312. 戳气球

​

312. 戳气球

作者：dp 加加

这是一道比较难且巧妙的动态规划题目；这道题目并不适合初学者看，比较适合 dp 进阶选手研究。好了，废话不多说，直接上菜。

题目描述

有 n 个气球，编号为0 到 n-1，每个气球上都标有一个数字，这些数字存在数组 nums 中。

现在要求你戳破所有的气球。每当你戳破一个气球 i 时，你可以获得 nums[left] * nums[i] * nums[right] 个硬币。 这里的 left 和 right 代表和 i 相邻的两个气球的序号。注意当你戳破了气球 i 后，气球 left 和气球 right 就变成了相邻的气球。

求所能获得硬币的最大数量。

说明:

你可以假设 nums[-1] = nums[n] = 1，但注意它们不是真实存在的所以并不能被戳破。
0 ≤ n ≤ 500, 0 ≤ nums[i] ≤ 100
示例:

输入: [3,1,5,8]
输出: 167
解释: nums = [3,1,5,8] --> [3,5,8] -->   [3,8]   -->  [8]  --> []
     coins =  3*1*5      +  3*5*8    +  1*3*8      + 1*8*1   = 167

思路

回溯法

分析一下这道题，就是要截破所有的气球，获得硬币的最大数量，然后左右两边的气球相邻了。那就截呗，我的第一反应就是暴力，回溯法；但是肯定会超时，为什么呢？因为题目给的气球数量有点多，最多 500 个；500 的阶乘，会超时爆栈；但是我们依然写一下代码，找下突破口，小伙伴们千万不要看不起暴力，暴力是优化的突破口；如果小伙伴对回溯法不太熟悉，我建议你记住下面的模版，也可以看我之前写的文章，回溯法基本可以使用以下的模版写。回溯法省心省力，0 智商负担，懂的朋友都懂，QAQ。

代码

var maxCoins = function (nums) {
  let res = Number.MIN_VALUE;
  backtrack(nums, 0);
  return res;
  // 回溯法，状态树很大
  function backtrack(nums, score) {
    if (nums.length == 0) {
      res = Math.max(res, score);
      return;
    }
    for (let i = 0, n = nums.length; i < n; i++) {
      let point =
        (i - 1 < 0 ? 1 : nums[i - 1]) *
        nums[i] *
        (i + 1 >= n ? 1 : nums[i + 1]);
      let tempNums = [].concat(nums);
      // 做选择 在 nums 中删除元素 nums[i]
      nums.splice(i, 1);
      // 递归回溯
      backtrack(nums, score + point);
      // 撤销选择
      nums = [...tempNums];
    }
  }
};

动态规划

回溯法的缺点也很明显，复杂度很高，对应本题截气球；小伙伴们可以脑补一下执行过程的状态树，这里我偷个懒就不画了；通过仔细观察这个状态树，我们会发现这个状态树的【选择】上，会有一些重复的选择分支；很明显存在了重复子问题；自然我就想到了能不能用动态规划来解决；

判读能不能用动态规划解决，还有一个问题，就是必须存在最优子结构；什么意思呢？其实就是根据局部最优，推导出答案；假设我们截破第 k 个气球是最优策略的最后一步，和上一步有没有联系呢？根据题目意思，截破第 k 个，前一个和后一个就变成相邻的了，看似是会有联系，其实是没有的。因为截破第 k 个和 k-1 个是没有联系的，脑补一下回溯法的状态树就更加明确了；

既然用动态规划，那就老套路了，把动态规划的三个问题想清楚定义好；然后找出题目的【状态】和【选择】，然后根据【状态】枚举，枚举的过程中根据【选择】计算递推就能得到答案了。

那本题的【选择】是什么呢？就是截哪一个气球。那【状态】呢？就是题目给的气球数量。

1. 定义状态

• 这里有个细节，就是题目说明有两个虚拟气球，nums[-1] = nums[n] = 1；如果当前截破的气球是最后一个或者第一个，前面/后面没有气球了，不能乘以 0，而是乘以 1。
• 定义状态的最关键两个点，往子问题（问题规模变小）想，最后一步最优策略是什么；我们假设最后截破的气球是 k，截破 k 获得最大数量的银币就是 nums[i] _ nums[k] _ nums[j] 再加上前面截破的最大数量和后面的最大数量，即：nums[i] _ nums[k] _ nums[j] + 前面最大数量 + 后面最大数量，就是答案。
• 而如果我们不考虑两个虚拟气球而直接定义状态，截到最后两个气球的时候又该怎么定义状态来避免和前面的产生联系呢？这两个虚拟气球就恰到好处了，太细节了；这也是本题的一个难点之一。
• 那我们可以这样来定义状态，dp[i][j] = x 表示，戳破气球 i 和气球 j 之间（开区间，不包括 i 和 j）的所有气球，可以获得的最大硬币数为 x。为什么开区间？因为不能和已经计算过的产生联系，我们这样定义之后，利用两个虚拟气球，截到最后两个气球的时候就完美的避开了所有状态的联系，太细节了。

1. 状态转移方程

• 而对于 dp[i][j]，i 和 j 之间会有很多气球，到底该截哪个先呢？我们直接设为 k，枚举选择最优的 k 就可以了。
• 所以，最终的状态转移方程为：dp[i][j] = max(dp[i][j], dp[i][k] + dp[k][j] + nums[k] + nums[i] + nums[j])

1. 初始值和边界

• 由于我们利用了两个虚拟气球，边界就是气球数 n + 2
• 初始值，当 i == j 时，很明显两个之间没有气球，所有为 0；

1. 如何枚举状态

• 因为我们最终要求的答案是 dp[0][n + 1]，就是截破虚拟气球之间的所有气球获得的最大值；
• 当 i == j 时，i 和 j 之间是没有气球的，所以枚举的状态很明显是 dp table 的左上部分，也就是 j 大于 i，如下图所示，只给出一部分方便思考。

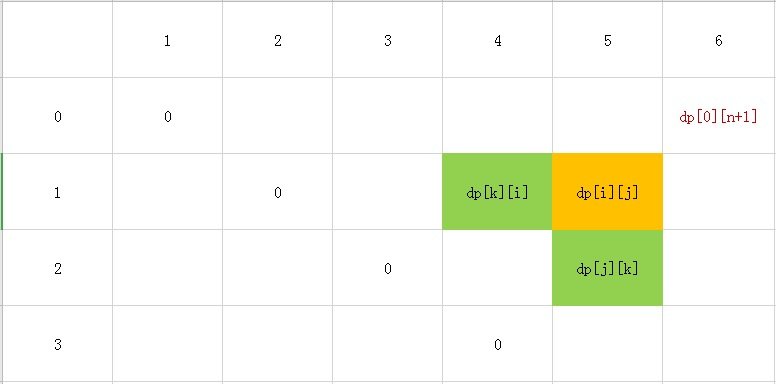
从上图可以看出，我们需要从下到上，从左到右进行遍历。

代码

var maxCoins = function (nums) {
  let n = nums.length;
  // 添加两侧的虚拟气球
  let points = [1, ...nums, 1];
  let dp = Array.from(Array(n + 2), () => Array(n + 2).fill(0));
  // 最后一行开始遍历,从下往上
  for (let i = n; i >= 0; i--) {
    // 从左往右
    for (let j = i + 1; j < n + 2; j++) {
      for (let k = i + 1; k < j; k++) {
        dp[i][j] = Math.max(
          dp[i][j],
          points[j] * points[k] * points[i] + dp[i][k] + dp[k][j]
        );
      }
    }
  }
  return dp[0][n + 1];
};

总结

简单的 dp 题目会直接告诉你怎么定义状态，告诉你怎么选择计算，你只需要根据套路判断一下能不能用 dp 解题即可，而判断能不能，往往暴力就是突破口。而困难点的 dp，我觉的都是细节问题了，要注意的细节太多了。感觉力扣加加，路西法大佬，把我领进了动态规划的大门，共勉。