lucifer

一维前缀和很容易求，那二维前缀和你会吗？

什么是前缀和？

前缀和是一种重要的预处理，能大大降低查询的时间复杂度。我们可以简单理解为“数列的前 n 项的和”。这个概念其实很容易理解，即一个数组中，第 n 位存储的是数组前 n 个数字的和。

通过一个例子来进行说明会更清晰。题目描述：有一个长度为 N 的整数数组 A，要求返回一个新的数组 B，其中 B 的第 i 个数 B[i]是原数组 A 前 i 项和。

这道题实际就是让你求数组 A 的前缀和。对 [1,2,3,4,5,6] 来说，其前缀和可以是 pre=[1,3,6,10,15,21]。我们可以使用公式 pre[𝑖]=pre[𝑖−1]+nums[𝑖]得到每一位前缀和的值，从而通过前缀和进行相应的计算和解题。其实前缀和的概念很简单，但困难的是如何在题目中使用前缀和以及如何使用前缀和的关系来进行解题。实际的题目更多不是直接让你求前缀和，而是你需要自己使用前缀和来优化算法的某一个性能瓶颈。

而如果数组是正数的话，前缀和数组会是一个单调不递减序列，因此前缀和 + 二分也会是一个考点，不过这种题目难度一般是力扣的困难难度。关于这个知识点，我会在之后的二分专题方做更多介绍。

简单的二维前缀和

上面提到的例子是一维数组的前缀和，简称一维前缀和。那么二维前缀和实际上就是二维数组上的前缀和了。一维数组的前缀和也是一个一维数组，同样地，二维数组的前缀和也是一个二维的数组。

比如对于如下的一个二维矩阵：

1
2
1 2 3 4
5 6 7 8

定义二维前缀和矩阵 $pres$，$pres{x,y} = \sum\limits_{i=1}^x \sum\limits_{j=1}^y a_{i,j}$。经过这样的处理，上面矩阵的二维前缀和就变成了：

1
2
1  3  6 10
6 14 24 36

那么如何用代码计算二维数组的前缀和呢？简单的二维前缀和的求解方法是基于容斥原理的。

比如我们想求如图中灰色部分的和。

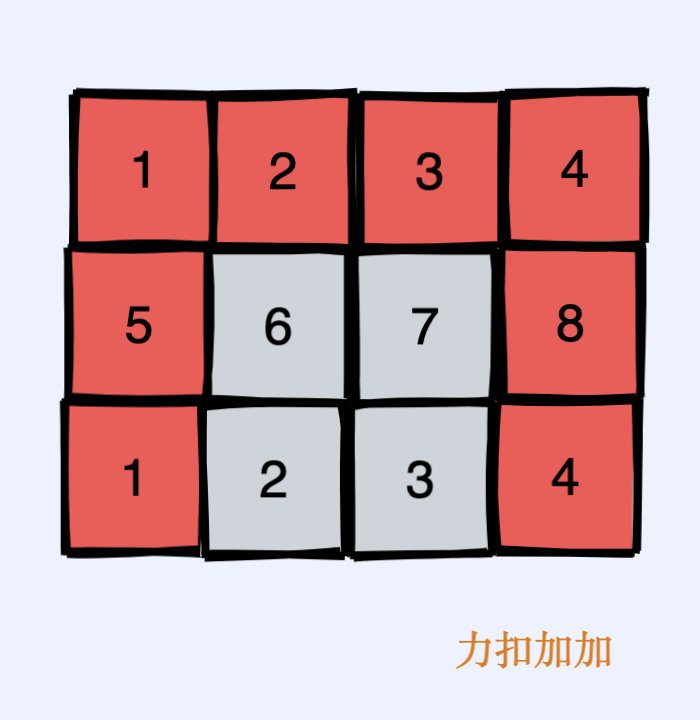
一种方式就是用下图中两个绿色部分的矩阵加起来（之所以用绿色部分相加是因为这两部分已经通过上面预处理计算好了，可以在 $O(1)$ 的时间得到），这样我们就会多加一块区域，这块区域就是如图黄色部分，我们再减去黄色部分就好了，最后再加上当前位置本身就行了。

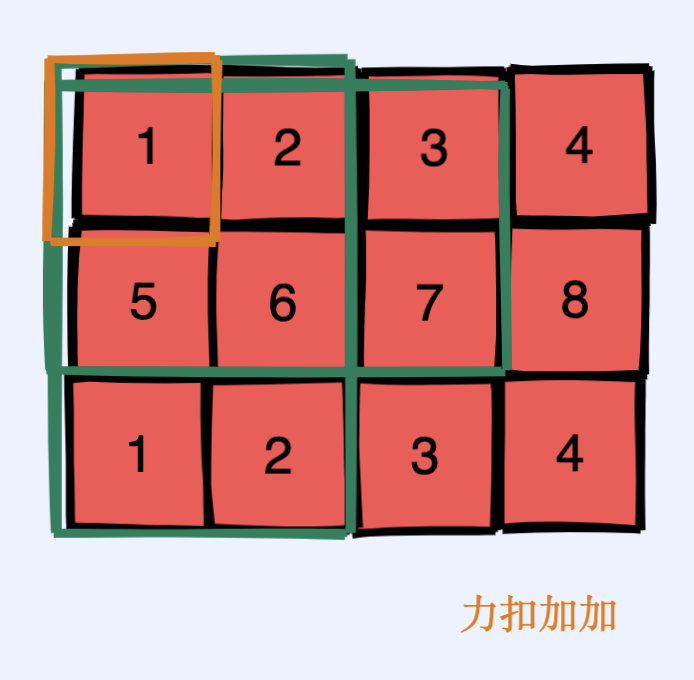
比如我们想要求 $sum_{i,j}$，则可以通过 $sum_{i - 1,j} + sum_{i,j - 1} - sum_{i - 1,j - 1} + a_{i,j}$ 的方式来实现。这样我就可以通过 $O(m n)$ 的预处理计算二维前缀和矩阵（m 和 n 分别为矩阵的长和宽），再通过 $O(1)$ 的时间计算出*任意小矩阵的和。其底层原理就是上面提到的容斥原理，大家可以通过画图的方式来感受一下。

如何将二维前缀和转化为一维前缀和

然而实际上，我们也可不构建一个前缀和数组，而是直接原地修改。

一维前缀和同样可以采用这一技巧。

比如我们可以先不考虑行之间的关联，而是预先计算出每一行的前缀和。对于计算每一行的前缀和就是一维前缀和啦。接下来通过固定两个列的端点的方式计算每一行的区域和。代码上，我们可以通过三层循环来实现， 其中两层循环用来固定列端点，另一层用于枚举所有行。

其实也可以反过来。即固定行的左右端点并枚举列，下面的题目会提到这一点。

代码表示：

1
2
3
4
# 预先构建行的前缀和
for row in matrix:
    for i in range(n - 1):
        row[i + 1] += row[i]

比如矩阵：

1
2
1 2 3 4
5 6 7 8

则会变为：

1
2
1 3 6 10
5 11 18 26

接下来：

1
2
3
4
5
6
7
8
9
10
# 固定列的两个端点，即枚举所有列的组合
for i in range(n):
    for j in range(i, n):
        pres = [0]
        pre = 0
        # 枚举所有行
        for k in range(m):
            # matrix[k] 其实已经是上一步预处理的每一行的前缀和了。因此 matrix[k][j] - (matrix[k][i - 1] 就是每一行 [i, j] 的区域和。
            pre += matrix[k][j] - (matrix[k][i - 1] if i > 0 else 0)
            pres.append(pre)

上面代码做的事情形象来看，就是先在水平方向计算前缀和，然后在竖直方向计算前缀和，而不是同时在两个方向计算。

如果把 [i, j] 的区域和看出是一个数的话，问题就和一维前缀和一样了。代码：

1
2
3
4
5
6
7
8
9
10

for i in range(n):
    for j in range(i, n):
        pres = [0]
        pre = 0
        # 枚举所有行
        for k in range(m):
            # 其中 a 为[i, j] 的区域和
            pre += a
            pres.append(pre)

题目推荐

有了上面的知识，我们就可以来解决下面两道题。虽然下面两道题的难度都是 hard，不过总体难度并不高。这两道题之所以是 hard， 是因为其考察了不止一个知识点。这也是 hard 题目的一种类型，即同时考察多个知识点。

363. 矩形区域不超过 K 的最大数值和

题目地址

https://leetcode-cn.com/problems/max-sum-of-rectangle-no-larger-than-k/

题目描述

1
2
3
4
5
6
7
8
9
10
11
12
13
给定一个非空二维矩阵 matrix 和一个整数 k，找到这个矩阵内部不大于 k 的最大矩形和。

示例:

输入: matrix = [[1,0,1],[0,-2,3]], k = 2
输出: 2
解释: 矩形区域 [[0, 1], [-2, 3]] 的数值和是 2，且 2 是不超过 k 的最大数字（k = 2）。


说明：

矩阵内的矩形区域面积必须大于 0。
如果行数远大于列数，你将如何解答呢？

前置知识

  • 二维前缀和
  • 二分法

思路

前面提到了由于非负数数组的二维前缀和是一个非递减的数组，因此常常和二分结合考察。实际上即使数组不是非负的，我们仍然有可能构建一个有序的前缀和，从而使用二分，这道题就是一个例子。

首先我们可以用上面提到的技巧计算二维数组的前缀和，这样我们就可以计算快速地任意子矩阵的和了。注意到上面我们计算的 pres 数组是一个一维数组，但矩阵其实可能为负数，因此不满足单调性。这里我们可以手动维护 pres 单调递增，这样就可以使用二分法在 $logN$ 的时间求出以当前项 i 结尾的不大于 k 的最大矩形和，那么答案就是所有的以任意索引 x 结尾的不大于 k 的最大矩形和的最大值。

之所以可以手动维护 pres 数组单调增也可得到正确结果的原因是题目只需要求子矩阵和，而不是求具体的子矩阵。

代码上，当计算出 pres 后，我们其实需要寻找大于等于 pre - k 的最小数 x。这样矩阵和 pre - x 才能满足 pre - x <= k，使用最左插入二分模板即可解决。

关键点

  • 典型的二维前缀和 + 二分题目

代码

  • 语言支持：Python3

Python3 Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

from sortedcontainers import SortedList


class Solution:
    def maxSumSubmatrix(self, matrix: List[List[int]], K: int) -> int:
        m, n = len(matrix), len(matrix[0])
        for i in range(m):
            for j in range(1, n):
                matrix[i][j] += matrix[i][j - 1]
        ans = float("-inf")
        for i in range(n):
            for j in range(i, n):
                pres = SortedList([0])
                pre = 0
                for k in range(m):
                    pre += matrix[k][j] - (0 if i == 0 else matrix[k][i - 1])
                    # 寻找小于等于 pre - k 的最大数。
                    # 为了达到这个目的，可以使用 bisect_left 来完成。（使用 bisect_right 不包含等号）
                    idx = pres.bisect_left(pre - K)
                    # 如果 i == len(pre) 表示无解
                    if idx < len(pres):
                        ans = max(ans, pre - pres[idx])
                    pres.add(pre)

        return ans

复杂度分析

令 n 为数组长度。

  • 时间复杂度：$O(m*n ^ 2logm)$
  • 空间复杂度：$O(m)$

题目给了一个 follow up：如果行数远大于列数，你将如何解答呢？ 实际上，如果行数远大于列数，由复杂度分析可知空间复杂度会很高。我们可以将行列兑换，这样空间复杂度是 $O(n)$。换句话说，我们可以通过行列的调换做到空间复杂度为 $O(min(m, n))$。

1074. 元素和为目标值的子矩阵数量

题目地址

https://leetcode-cn.com/problems/number-of-submatrices-that-sum-to-target/

题目描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
给出矩阵 matrix 和目标值 target，返回元素总和等于目标值的非空子矩阵的数量。

子矩阵 x1, y1, x2, y2 是满足 x1 <= x <= x2 且 y1 <= y <= y2 的所有单元 matrix[x][y] 的集合。

如果 (x1, y1, x2, y2) 和 (x1', y1', x2', y2') 两个子矩阵中部分坐标不同（如：x1 != x1'），那么这两个子矩阵也不同。

 

示例 1：

输入：matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
输出：4
解释：四个只含 0 的 1x1 子矩阵。


示例 2：

输入：matrix = [[1,-1],[-1,1]], target = 0
输出：5
解释：两个 1x2 子矩阵，加上两个 2x1 子矩阵，再加上一个 2x2 子矩阵。


 

提示：

1 <= matrix.length <= 300
1 <= matrix[0].length <= 300
-1000 <= matrix[i] <= 1000
-10^8 <= target <= 10^8

前置知识

  • 二维前缀和

思路

和上面题目类似。不过这道题是求子矩阵和刚好等于某个目标值的数目。

我们不妨先对问题进行简化。比如题目要求的是一维数组中，子数组（连续）的和等于目标值 target 的数目。我们该如何做？

这很容易，我们只需要：

  • 边遍历边计算前缀和。
  • 比如当前的前缀和是 cur，那么我们要找的前缀和 x 应该满足 cur - x = target，因为这样当前位置和 x 的之间的子数组和才是 target。即我们需要找前缀和为 cur - target 的数目。 这提示我们使用哈希表记录每一种前缀和出现的次数。

由于仅仅是求数目，不涉及到求具体的子矩阵信息，因此使用类似上面的解法求出二维前缀和。接下来，使用和一维前缀和同样的方法即可求出答案。

关键点

  • 主要考察一维前缀和到二维前缀和的过渡是否掌握

代码

  • 语言支持：Python3

Python3 Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

class Solution:
    def numSubmatrixSumTarget(self, matrix, target):
        m, n = len(matrix), len(matrix[0])
        for row in matrix:
            for i in range(n - 1):
                row[i + 1] += row[i]
        ans = 0
        for i in range(n):
            for j in range(i, n):
                c = collections.defaultdict(int)
                cur, c[0] = 0, 1
                for k in range(m):
                    cur += matrix[k][j] - (matrix[k][i - 1] if i > 0 else 0)
                    ans += c[cur - target]
                    c[cur] += 1
        return ans

复杂度分析

  • 时间复杂度：$O(m * n ^ 2)$
  • 空间复杂度：$O(m)$

和上面一样，我们可以将行列对换，这样空间复杂度是 $O(n)$。换句话说，我们可以通过行列的调换做到空间复杂度为 $O(min(m, n))$。

更多题目

这道题就是二维前缀和 + 一维最大子序和的知识就可以 AC。而这两个西法我都写过文章了，不懂的建议看看。

参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution:
    def getMaxMatrix(self, matrix: List[List[int]]) -> List[int]:
        max_area = float("-inf")
        ans = []
        m, n = len(matrix), len(matrix[0])

        for i in range(m):
            for j in range(1, n):
                matrix[i][j] += matrix[i][j - 1]

        for i in range(n):
            for j in range(i, n):
                pre = min_pre = min_pre_idx = 0
                for k in range(m):
                    if pre < min_pre:
                        min_pre = pre
                        min_pre_idx = k
                    pre += matrix[k][j] - (matrix[k][i - 1] if i > 0 else 0)
                    if pre - min_pre > max_area:
                        max_area = pre - min_pre
                        ans = [min_pre_idx, i, k, j]

        return ans

力扣的小伙伴可以关注我，这样就会第一时间收到我的动态啦~

以上就是本文的全部内容了。大家对此有何看法，欢迎给我留言，我有时间都会一一查看回答。更多算法套路可以访问我的 LeetCode 题解仓库：https://github.com/azl397985856/leetcode 。 目前已经 40K star 啦。大家也可以关注我的公众号《力扣加加》带你啃下算法这块硬骨头。


 上一页

数据结构 算法 数学 最大公约数

 评论


博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本站使用 Material X 作为主题 。
载入天数...载入时分秒...