lucifer

我在动态规划专题反复强调了先学习递归，再学习记忆化，最后再学动态规划。

其中原因已经讲得很透了，相信大家已经明白了。如果不明白，强烈建议先看看那篇文章。

尽管很多看了我文章的小伙伴知道了先去学记忆化递归，但是还是有一些粉丝问我：“记忆化递归转化为动态规划老是出错，不得要领怎么办？有没有什么要领呀？”

今天我就来回答一下粉丝的这个问题。

实际上我的动态规划那篇文章已经讲了将记忆化递归转化为动态规划的大概的思路，只是可能不是特别细，今天我们就尝试细化一波。

我们仍然先以经典的爬楼梯为例，给大家讲一点基础知识。接下来，我会带大家解决一个更加复杂的题目。

爬楼梯

题目描述

一个人爬楼梯，每次只能爬 1 个或 2 个台阶，假设有 n 个台阶，那么这个人有多少种不同的爬楼梯方法？

思路

由于第 n 级台阶一定是从 n - 1 级台阶或者 n - 2 级台阶来的，因此到第 n 级台阶的数目就是 到第 n - 1 级台阶的数目加上到第 n - 1 级台阶的数目。

记忆化递归代码：

1
2
3
4
5
6
7
8
9
10
11
const memo = {};
function climbStairs(n) {
  if (n === 1) return 1;
  if (n === 2) return 2;
  if (n in memo) return memo[n];
  ans = climbStairs(n - 1) + climbStairs(n - 2);
  memo[n] = ans;
  return ans;
}

climbStairs(10);

首先为了方便看出关系，我们先将 memo 的名字改一下，将 memo 换成 dp：

{1,5,7}
1
2
3
4
5
6
7
8
9
10
11
const dp = {};
function climbStairs(n) {
  if (n === 1) return 1;
  if (n === 2) return 2;
  if (n in dp) return dp[n];
  ans = climbStairs(n - 1) + climbStairs(n - 2);
  dp[n] = ans;
  return ans;
}

climbStairs(10);

其他地方一点没动，就是名字改了下。

那么这个记忆化递归代码如何改造成动态规划呢？这里我总结了三个步骤，根据这三个步骤就可以将很多记忆化递归轻松地转化为动态规划。

1. 根据记忆化递归的入参建立 dp 数组

在动态规划专题中，西法还提过动态规划的核心就是状态。动态规划问题时间复杂度打底就是状态数，空间复杂度如果不考虑滚动数组优化打底也是状态数，而状态数是什么？不就是各个状态的取值范围的笛卡尔积么？而状态正好对应的就是记忆化递归的入参。

对应这道题，显然状态是当前位于第几级台阶。那么状态数就有 n 个。因此开辟一个长度为 n 的一维数组就好了。

我用 from 表示改造前的记忆化递归代码， to 表示改造后的动态规划代码。（下同，不再赘述）

from:

1
2
dp = {};
function climbStairs(n) {}

to:

1
2
3
function climbStairs(n) {
  const dp = new Array(n);
}

2. 用记忆化递归的叶子节点返回值填充 dp 数组初始值

如果你模拟上面 dp 函数的执行过程会发现: if n == 1 return 1 和 if n == 2 return 2，对应递归树的叶子节点，这两行代码深入到叶子节点才会执行。接下来再根据子 dp 函数的返回值合并结果，是一个典型的后序遍历。

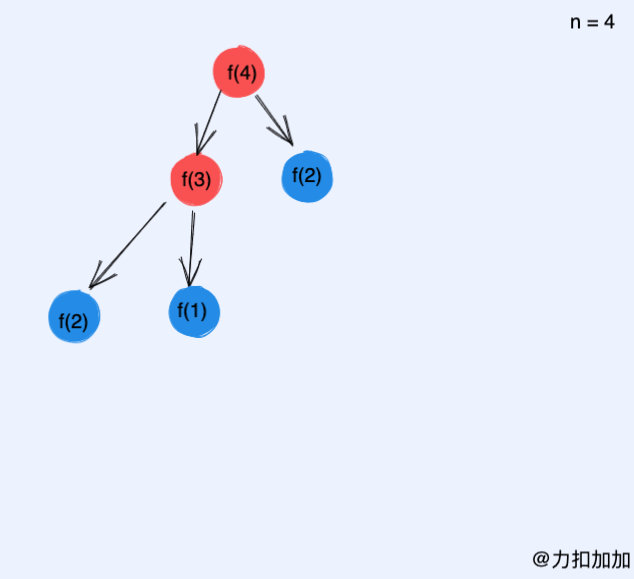
蓝色表示叶子节点

如果改造成迭代，如何做呢？一个朴素的想法就是从叶子节点开始模拟递归栈返回的过程，没错动态规划本质就是如此。从叶子节点开始，到根节点结束，这也是为什么记忆化递归通常被称为自顶向下，而动态规划被称为自底向上的原因。这里的底和顶可以看做是递归树的叶子和根。

知道了记忆化递归和动态规划的本质区别。 接下来，我们填充初始化，填充的逻辑就是记忆化递归的叶子节点 return 部分。

from:

1
2
3
4
5
const dp = {};
function climbStairs(n) {
  if (n == 1) return 1;
  if (n == 2) return 2;
}

to:

1
2
3
4
5
function climbStairs(n) {
  const dp = new Array(n);
  dp[0] = 1;
  dp[1] = 2;
}

dp 长度为 n，索引范围是 [0,n-1]，因此 dp[n-1] 对应记忆化递归的 dp(n)。因此 dp[0] = 1 等价于上面的 if n == 1: return 1。 如果你想让二者完全对应也是可以的，数组长度开辟为 n + 1，并且数组索引 0 不用即可。

3. 枚举笛卡尔积，并复制主逻辑

  1. if (xxx in dp) return dp[xxx] 这种代码删掉
  2. 将递归函数 f(xxx, yyy, …) 改成 dp[xxx][yyy][….] ，对应这道题就是 climbStairs(n) 改成 dp[n]
  3. 将递归改成迭代。比如这道题每次 climbStairs(n) 递归调用了 climbStairs(n-1) 和 climbStairs(n-2)，一共调用 n 次，我们要做的就是迭代模拟。比如这里调用了 n 次，我们就用一层循环来模拟执行 n 次。如果有两个参数就两层循环，三个参数就三层循环，以此类推。

from:

1
2
3
4
5
6
7
8
const dp = {};
function climbStairs(n) {
  // ...
  if (n in dp) return dp[n];
  ans = climbStairs(n - 1) + climbStairs(n - 2);
  dp[n] = ans;
  return ans;
}

to:

1
2
3
4
5
6
7
8
function climbStairs(n) {
  // ...
  // 这个循环其实就是咱上面提到的状态的笛卡尔积。由于这道题就一个状态，枚举一层就好了。如果状态有两个，那么笛卡尔积就可以用两层循环搞定。至于谁在外层循环谁在内层循环，请看我的动态规划专题。
  for (let i = 2; i < n; i++) {
    dp[i] = dp[i - 1] + dp[i - 2];
  }
  return dp[dp.length - 1];
}

将上面几个步骤的成果合并起来就可以将原有的记忆化递归改造为动态规划了。

完整代码：

1
2
3
4
5
6
7
8
9
10
11
function climbStairs(n) {
  if (n == 1) return 1;
  const dp = new Array(n);
  dp[0] = 1;
  dp[1] = 2;

  for (let i = 2; i < n; i++) {
    dp[i] = dp[i - 1] + dp[i - 2];
  }
  return dp[dp.length - 1];
}

有的人可能觉得这道题太简单了。实际上确实有点简单了。 而且我也承认有的记忆化递归比较难以改写，什么情况记忆化递归比较好写，改成动态规划就比较麻烦我也在动态规划专题给大家讲过了，不清楚的同学翻翻。

据我所知，如果动态规划可以过，大多数记忆化递归都可以过。有一些极端情况记忆化递归过不了：那就是力扣测试用例偏多，并且数据量大的测试用例比较多。这是由于力扣的超时判断是多个测试用例的用时总和，而不是单独计算时间。

接下来，我再举一个稍微难一点的例子（这个例子就必须使用动态规划才能过，记忆化递归会超时）。带大家熟悉我上面给大家的套路。

1824. 最少侧跳次数

题目描述

1
2
3
4
5
6
7
8
9
10
11
12
13
给你一个长度为  n  的  3 跑道道路  ，它总共包含  n + 1  个   点  ，编号为  0  到  n 。一只青蛙从  0  号点第二条跑道   出发  ，它想要跳到点  n  处。然而道路上可能有一些障碍。

给你一个长度为 n + 1  的数组  obstacles ，其中  obstacles[i] （取值范围从 0 到 3）表示在点 i  处的  obstacles[i]  跑道上有一个障碍。如果  obstacles[i] == 0 ，那么点  i  处没有障碍。任何一个点的三条跑道中   最多有一个   障碍。

比方说，如果  obstacles[2] == 1 ，那么说明在点 2 处跑道 1 有障碍。
这只青蛙从点 i  跳到点 i + 1  且跑道不变的前提是点 i + 1  的同一跑道上没有障碍。为了躲避障碍，这只青蛙也可以在   同一个   点处   侧跳   到 另外一条   跑道（这两条跑道可以不相邻），但前提是跳过去的跑道该点处没有障碍。

比方说，这只青蛙可以从点 3 处的跑道 3 跳到点 3 处的跑道 1 。
这只青蛙从点 0 处跑道 2  出发，并想到达点 n  处的 任一跑道 ，请你返回 最少侧跳次数  。

注意：点 0  处和点 n  处的任一跑道都不会有障碍。

示例 1：

1
2
3
4
5
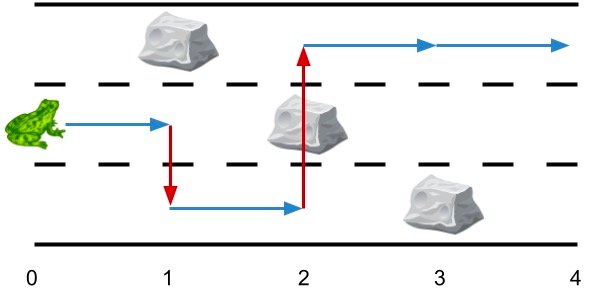
输入：obstacles = [0,1,2,3,0]
输出：2
解释：最优方案如上图箭头所示。总共有 2 次侧跳（红色箭头）。
注意，这只青蛙只有当侧跳时才可以跳过障碍（如上图点 2 处所示）。
示例 2：

1
2
3
4
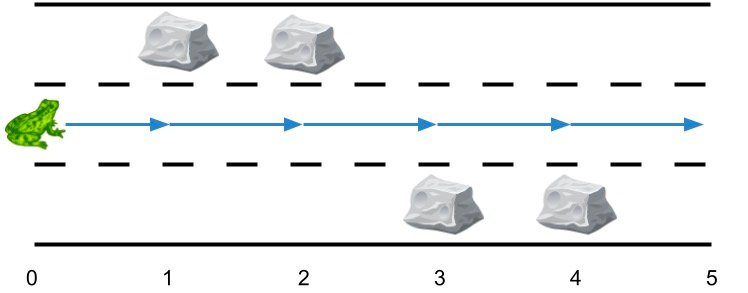
输入：obstacles = [0,1,1,3,3,0]
输出：0
解释：跑道 2 没有任何障碍，所以不需要任何侧跳。
示例 3：

1
2
3
4
5
6
7
8
9
10
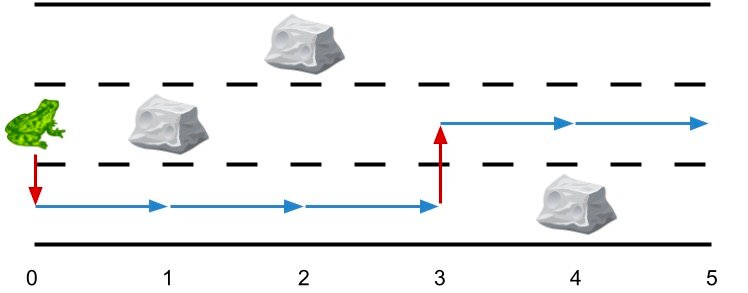
输入：obstacles = [0,2,1,0,3,0]
输出：2
解释：最优方案如上图所示。总共有 2 次侧跳。

提示：

obstacles.length == n + 1
1 <= n <= 5 \* 105
0 <= obstacles[i] <= 3
obstacles[0] == obstacles[n] == 0

思路

这个青蛙在反复横跳？？

稍微解释一下这个题目。

  • 如果当前跑道后面一个位置没有障碍物，这种情况左右横跳一定不会比直接平跳更优，我们应该贪心地直接平跳（不是横跳）过去。这是因为最坏情况我们可以先平跳过去再横跳，这和先横跳再平跳是一样的。

  • 如果当前跑道后面一个位置有障碍物，我们需要横跳到一个没有障碍物的通道，同时横跳计数器 + 1。

最后选取所有到达终点的横跳次数最少的即可，对应递归树中就是到达叶子节点时计数器最小的。

使用 dp(pos, line) 表示当前在通道 line， 从 pos 跳到终点需要的最少的横跳数。不难写出如下记忆化递归代码。

由于本篇文章主要讲的是记忆化递归改造动态规划，因此这道题的细节就不多介绍了，大家看代码就好。

我们来看下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution:
    def minSideJumps(self, obstacles: List[int]) -> int:
        dp = {}
        def f(pos, line):
            if (pos, line) in dp: return dp[(pos, line)]
            if pos == len(obstacles) - 1:
                return 0
            # 贪心地平跳
            if obstacles[pos + 1] != line:
                ans = f(pos + 1, line)
                dp[(pos, line)] = ans
                return ans
            ans = float("inf")
            for nxt in [1, 2, 3]:
                if nxt != line and obstacles[pos] != nxt:
                    ans = min(ans, 1 +f(pos, nxt))
            dp[(pos, line)] = ans
            return ans

        return f(0, 2)

这道题记忆化递归会超时，需要使用动态规划才行。 那么如何将 ta 改造成动态规划呢？

还是用上面的口诀。

1. 根据记忆化递归的入参建立 dp 数组

上面递归函数的是 dp(pos, line)，状态就是形参，因此需要建立一个 m * n 的二维数组，其中 m 和 n 分别是 pos 和 line 的取值范围集合的大小。而 line 取值范围其实就是 [1,3]，为了方便索引对应，这次西法决定浪费一个空间。由于这道题是求最小，因此初始化为无穷大没毛病。

from:

1
2
3
4
5
6
7
class Solution:
    def minSideJumps(self, obstacles: List[int]) -> int:
        dp = {}
        def f(pos, line):
            # ...

        return f(0, 2)

to:

1
2
3
4
5
class Solution:
    def minSideJumps(self, obstacles: List[int]) -> int:
        dp = [[float("inf")] * 4 for _ in range(len(obstacles))]
        # ...
        return min(dp[-1])

2. 用记忆化递归的叶子节点返回值填充 dp 数组初始值

不多说了，直接上代码。

from:

1
2
3
4
5
6
7
8
9
class Solution:
    def minSideJumps(self, obstacles: List[int]) -> int:
        dp = {}
        def f(pos, line):
            if pos == len(obstacles) - 1:
                return 0
            # ...

        return f(0, 2)

to:

1
2
3
4
5
6
class Solution:
    def minSideJumps(self, obstacles: List[int]) -> int:
        dp = [[float("inf")] * 4 for _ in range(len(obstacles))]
        dp[0] = [0, 1, 0, 1]
        # ...
        return min(dp[-1])

3. 枚举笛卡尔积，并复制主逻辑

这道题如何枚举状态？当然是枚举状态的笛卡尔积了。简单，几个状态就几层循环呗。

上代码。

1
2
3
4
5
6
7
8
class Solution:
    def minSideJumps(self, obstacles: List[int]) -> int:
        dp = [[float("inf")] * 4 for _ in range(len(obstacles))]
        dp[0] = [0, 1, 0, 1]
        for pos in range(1, len(obstacles)):
            for line in range(1, 4):
                # ...
        return min(dp[-1])

接下来就是把记忆化递归的主逻辑复制一下粘贴过来就行。

from:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    def minSideJumps(self, obstacles: List[int]) -> int:
        dp = {}
        def f(pos, line):
            # ...
            # 贪心地平跳
            if obstacles[pos + 1] != line:
                ans = f(pos + 1, line)
                dp[(pos, line)] = ans
                return ans
            ans = float("inf")
            for nxt in [1, 2, 3]:
                if nxt != line and obstacles[pos] != nxt:
                    ans = min(ans, 1 +f(pos, nxt))
            dp[(pos, line)] = ans
            return ans

        return f(0, 2)

to：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def minSideJumps(self, obstacles: List[int]) -> int:
        dp = [[float("inf")] * 4 for _ in range(len(obstacles))]
        dp[0] = [0, 1, 0, 1]
        for pos in range(1, len(obstacles)):
            for line in range(1, 4):
                if obstacles[pos - 1] != line: # 由于自底向上，因此是和 pos - 1 建立联系，而不是 pos + 1
                    dp[pos][line] = min(dp[pos][line], dp[pos - 1][line])
                else:
                    for nxt in range(1, 4):
                        if nxt != line and obstacles[pos] != nxt:
                            dp[pos][line] = min(dp[pos][line], 1 + dp[pos][nxt])

        return min(dp[-1])

可以看出我基本就是把主逻辑复制过来，稍微改改。 改的基本就是因为：

  • 之前是递归函数，因此 return 需要去掉，比如改成 continue 啥的，不能让函数直接返回，而是继续枚举下一个状态。
  • 之前是 dp[(pos, line)] = ans 现在则改成填充咱上面初始好的二维 dp 数组。

你以为这就结束了么？

那你就错了。之所以选这道题是有原因的。这道题直接提交会报错，是答案错误（WA）。

这里我要告诉大家的是：由于我们使用迭代模拟递归过程，使用多层循环枚举状态的笛卡尔积，而主逻辑部分则是状态转移方程，而转移方程的书写和枚举的顺序息息相关。

从代码不难看出：对这道题来说我们采用的是从小到大枚举，而 dp[pos][line] 也仅仅依赖 dp[pos-1][line] 和 dp[pos][nxt]。

而问题的关键是 nxt，比如处理到了 dp[2][1]，d[2][1] 依赖了 dp[2][3] 的值，而实际上 dp[2][3] 是没有处理到的。

因此上面动态规划的的这一行代码有问题：

1
dp[pos][line] = min(dp[pos][line], 1 + dp[pos][nxt])

因为遍历到 dp[pos][line] 的时候，有可能 dp[pos][nxt] 还没计算好(没有枚举到)，这就是产生了 bug。

那为什么记忆化递归就没问题呢？

其实很简单。递归函数里面的子问题都是没有计算好的，到叶子节点后再开始计算，计算好后往上返回，而返回的过程其实和迭代是类似的。

比如这道题的 f(0,2) 的递归树大概是这样的，其中虚线标识可能无法到达。

递归树

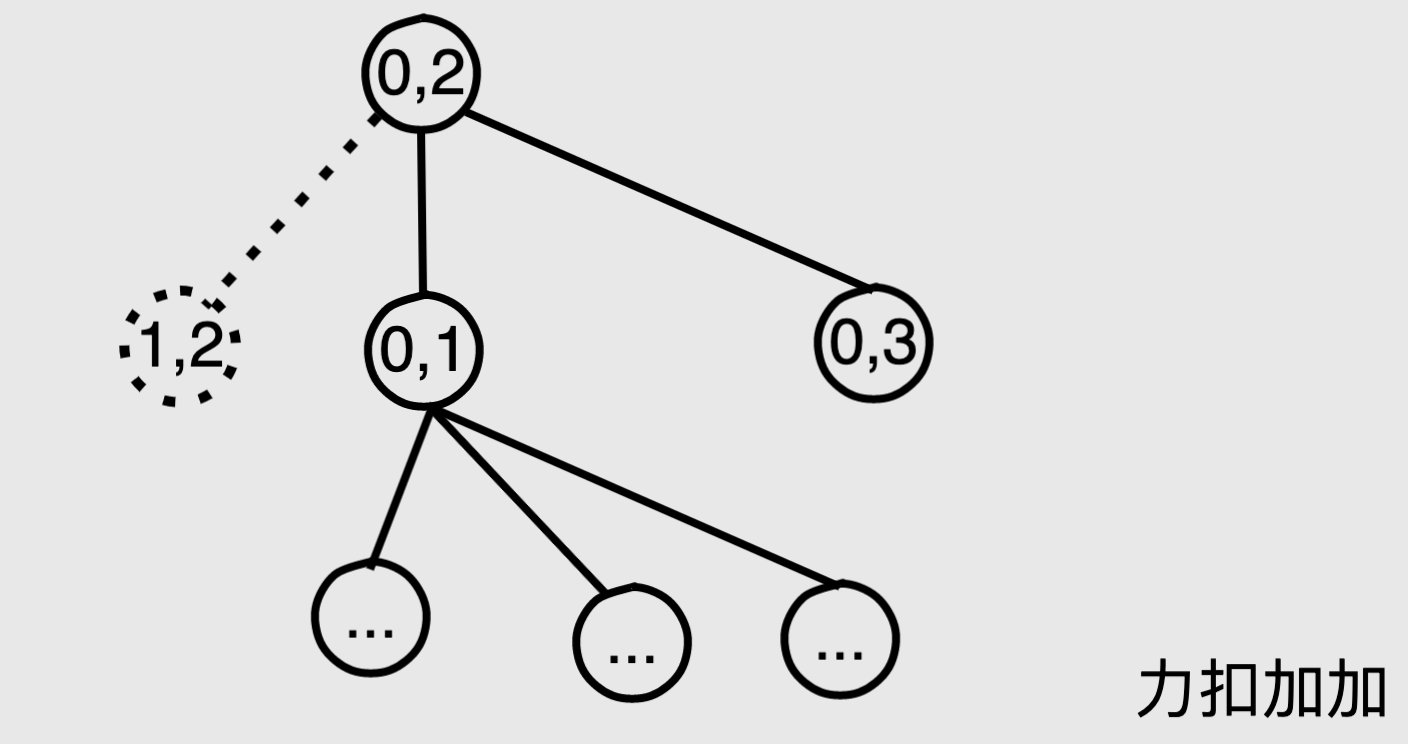
当从 f(0, 2) 递归到 f(0, 1) 或者 f(0, 3) 的的时候，都是没计算好的，因此都无所谓，代码会继续往叶子节点方向扩展，到达叶子节点返回后，所有的子节点肯定都已经计算好了，接下来的过程和普通的迭代就很像了。

比如 f(0,2) 递归到 f(0,3) ，f(0,3) 会继续向下递归知道叶子节点，然后向上返回，当再次回到 f(0,2) 的时候，f(0,3) 一定是已经计算好的。

形象点来说就是：f(0,2) 是一个 leader，告诉他的下属 f(0,3)，我想要 xxxx，怎么实现我不管，你有的话直接给我（记忆化），没有的话想办法获取（递归）。不管怎么样，反正你给我弄出来送到我手上。

而如果使用迭代的动态规划，你有的话直接给我（记忆化）很容易做到。关键是没有的话想办法获取（递归）不容易做到啊，至少需要一个类似的循环去完成吧？

那如何解决这个问题呢？

很简单，每次只依赖已经计算好的状态就好了。

对于这道题来说，虽然 dp[pos][nxt] 可能没计算好了，那么 dp[pos-1][nxt] 一定是计算好的，因为 dp[pos-1][nxt] 已经在上一次主循环计算好了。

但是直接改成 dp[pos-1][nxt] 逻辑还对么？这就要具体问题具体分析了，对于这道题来说，这么写是可以的。

这是因为这里的逻辑是如果当前赛道的前面一个位置有障碍物，那么我们不能从当前赛道的前一个位置过来，而只能选择从其他两个赛道横跳过来。

我画了一个简图。其中 X 表示障碍物，O 表示当前的位置，数字表示时间上的先后循序，先跳 1 再跳 2 。。。

1
2
3
-XO
---
---

在这里，而以下两种情况其实是等价的：

情况 1（也就是上面 dp[pos][nxt] 的情况）：

1
2
3
-X2
--1
---

情况 2（也就是上面 dp[pos-1][nxt] 的情况）：

1
2
3
-X3
-12
---

可以看出二者是一样的。没懂？多看看，多想想。

综上，我们将 dp[pos][nxt] 改成 dp[pos-1][nxt] 不会有问题。大家遇到其他问题也采取类似思路分析一波即可。

完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def minSideJumps(self, obstacles: List[int]) -> int:
        dp = [[float("inf")] * 4 for _ in range(len(obstacles))]
        dp[0] = [0, 1, 0, 1]
        for pos in range(1, len(obstacles)):
            for line in range(1, 4):
                if obstacles[pos - 1] != line: # 由于自底向上，因此是和 pos - 1 建立联系，而不是 pos + 1
                    dp[pos][line] = min(dp[pos][line], dp[pos - 1][line])
                else:
                    for nxt in range(1, 4):
                        if nxt != line and obstacles[pos] != nxt:
                            dp[pos][line] = min(dp[pos][line], 1 + dp[pos-1][nxt])

        return min(dp[-1])

趁热打铁再来一个

再来一个例子，1866. 恰有 K 根木棍可以看到的排列数目。

思路

直接上记忆化递归代码：

1
2
3
4
5
6
7
8
class Solution:
    def rearrangeSticks(self, n: int, k: int) -> int:
        @lru_cache(None)
        def dp(i, j):
            if i == 0 and j != 0: return 0
            if i == 0 and j == 0: return 1
            return (dp(i - 1, j - 1) + dp(i - 1, j) * (i - 1)) % (10**9 + 7)
        return dp(n, k) % (10**9 + 7)

咱不管这个题是啥，代码怎么来的。假设这个代码咱已经写出来了。那么如何改造成动态规划呢？继续套用三部曲。

1. 根据记忆化递归的入参建立 dp 数组

由于 i 的取值 [0-n] 一共 n + 1 个， j 的取值是 [0-k] 一共 k + 1 个。因此初始化一个二维数组即可。

1
dp = [[0] * (k+1) for _ in range(n+1)]

2. 用记忆化递归的叶子节点返回值填充 dp 数组初始值

由于 i == 0 and j == 0 是 1，因此直接写 dp[0][0] = 1 就好了。

{2}
1
2
dp = [[0] * (k+1) for _ in range(n+1)]
dp[0][0] = 1

3. 枚举笛卡尔积，并复制主逻辑

就是两层循环枚举 i 和 j 的所有组合就好了。

{4-6}
1
2
3
4
5
6
7
dp = [[0] * (k+1) for _ in range(n+1)]
dp[0][0] = 1

for i in range(1, n + 1):
    for j in range(1, min(k, i) + 1):
        # ...
return dp[-1][-1]

最后把主逻辑复制过来完工了。

比如： return xxx 改成 dp[形参一][形参二] = xxx 等小细节。

最终的一个代码就是：

{7-11}
1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def rearrangeSticks(self, n: int, k: int) -> int:
        dp = [[0] * (k+1) for _ in range(n+1)]
        dp[0][0] = 1

        for i in range(1, n + 1):
            for j in range(1, min(k, i) + 1):
                dp[i][j] = dp[i-1][j-1]
                if i - 1 >= j:
                    dp[i][j] += dp[i-1][j] * (i - 1)
                dp[i][j] %= 10**9 + 7
        return dp[-1][-1]

总结

有的记忆化递归比较难以改写，什么情况记忆化递归比较好写，改成动态规划就比较麻烦我也在动态规划专题给大家讲过了，不清楚的同学翻翻。

我之所以推荐大家从记忆化递归入手，正是因为很多情况下记忆化写起来简单，而且容错高（想想上面的青蛙跳的例子）。这是因为记忆化递归总是后序遍历，会在到达叶子节点只会往上计算。而往上计算的过程和迭代的动态规划是类似的。或者你也可以认为迭代的动态规划是在模拟记忆化递归的归的过程。

我们要做的就是把一些容易改造的方法学会，接下来面对难的尽量用记忆化递归。据我所知，如果动态规划可以过，大多数记忆化递归都可以过。有一个极端情况记忆化递归过不了：那就是力扣测试用例偏多，并且数据量大的测试用例比较多。这是由于力扣的超时判断是多个测试用例的用时总和，而不是单独计算时间。

将记忆化递归改造成动态规划可以参考我的这三个步骤：

  1. 根据记忆化递归的入参建立 dp 数组
  2. 用记忆化递归的叶子节点返回值填充 dp 数组初始值
  3. 枚举笛卡尔积，并复制主逻辑

另外有一点需要注意的是：状态转移方程的确定和枚举的方向息息相关，虽然不同题目细节差异很大。 但是我们只要牢牢把握一个原则就行了，那就是：永远不要用没有计算好的状态，而是仅适用已经计算好的状态。


 上一页

前端 面经

 评论


博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本站使用 Material X 作为主题 。
载入天数...载入时分秒...