lucifer

经过了半年时间打磨，投入诸多人力，这本 LeetCode 题解书终于要和大家见面了。
💐💐💐💐💐。

实体版购书链接：https://union-click.jd.com/jdc?e=618%7Cpc%7C&p=JF8BAN4JK1olXwUFU1xcAUoRA18IGFMXXgQDUG4ZVxNJXF9RXh5UHw0cSgYYXBcIWDoXSQVJQwYBXFxeCkoTHDZNRwYlQ1J3BB0EWEl0QhkIH1xMBXBlDyQ1TkcbM244G1oUXQ4HU1tbDXsnA2g4STXN67Da8e9B3OGY1uefK1olXQEEUFhYCkgSAWwOHmsSXQ8yDwszD0sSUDtbGAlCDVJVAW5tOEgnBG8BD11nHFQWUixtOEsnAF9KdV5AWQcDB1cPDktEAWpfSwhFXwUDUllVDkMVATxbHVwWbQQDVVpUOHs

电子版购书链接：https://union-click.jd.com/jdc?e=&p=JF8BAL0JK1olXDYAVVhfD04UAl9MRANLAjZbERscSkAJHTdNTwcKBlMdBgABFkkWBW0PHlgUQl9HCANtcS0SdTFvWVt1X3BkVV4Kc0JxYRtPe1cZbQcyVF9cCEMSBGoOHmslXQEyHzBcOEonA2gKE1oVWwEKXV5cAXsQA2Y4QA57WgYHBwoOCxlAUztfTmslbQUyZG5dOEgnQQFaSQ5FWQYFB1cODhgSVDpaS1hFDwQLUlwJAU5DAWcJHWsXXAcGXW4

在线试读

背景

自 LeetCode 题解 （现在已经接近 45k star 了）项目被大家开始关注，就有不少出版社开始联系我写书。刚开始后的时候，我并没有这个打算，觉得写这个相对于博客形式的题解要耗费时间，且并不一定效果比博客形式的效果好。后来当我向大家提及“出版社找我写书”这件事情的时候，很多人表示“想要买书，于是我就开始打算写这样一本书。但是一个完全没有写书经验的人，独立完成一本书工作量还是蛮大的，因此我打算寻求其他志同道合人士的帮助。

团队介绍

团队成员大都来自 985， 211 学校计算机系，大家经常参加算法竞赛，也坚持参加 LeetCode 周赛。在这个过程中，我们积累了很多经验，希望将这些经验分享给大家，以减少大家在刷题过程中的阻碍，让大家更有效率的刷题。 本书尤其适合那些刚刚开始刷题的人，如果你刚开始刷题，或者刷了很多题面对新题还是无法很好的解决，那么这本书肯定很适合你。最后欢迎大家加入我们的读者群和作者进行交流。

样张

这里给大家开放部分章节内容给大家，让大家尝尝鲜。当然也欢迎大家提出宝贵的建议，帮助我们写出更好的内容。

我们开放了第八章第五小节给大家看，以下是具体内容：

8.5 1206. 设计跳表

题目描述

不使用任何库函数，设计一个跳表。

跳表是在 $O(logN)$ 时间内完成增加、删除、搜索操作的数据结构。跳表相比于树堆与红黑树，其功能与性能相当，并且跳表的代码长度相较下更短，其设计思想与链表相似。

跳表中有很多层，每一层是一个短的链表。在第一层的作用下，增加、删除和搜索操作的时间复杂度不超过 $O(N)$。跳表的每一个操作的平均时间复杂度是 $O(logN)$，空间复杂度是 $O(N)$。

在本题中，你的设计应该要包含这些函数：

  • bool search(int target) : 返回 target 是否存在于跳表中。
  • void add(int num): 插入一个元素到跳表。
  • bool erase(int num): 在跳表中删除一个值，如果 num 不存在，直接返回 false. 如果存在多个 num ，删除其中任意一个即可。

注意，跳表中可能存在多个相同的值，你的代码需要处理这种情况。

样例：

1
2
3
4
5
6
7
8
9
10
11
Skiplist skiplist = new Skiplist();

skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0);   // 返回 false
skiplist.add(4);
skiplist.search(1);   // 返回 true
skiplist.erase(0);    // 返回 false，0 不在跳表中
skiplist.erase(1);    // 返回 true
skiplist.search(1);   // 返回 false，1 已被擦除

约束条件：
0 <= num, target <= 20000
最多调用 50000 次 search, add, 以及 erase 操作。

思路

首先，使用跳表会将数据存储成有序的。在数据结构当中，我们通常有两种基本的线性结构，结合有序数据，表达如下：

  • 有序链表，我们有三种基本操作：
    • 查找指定的数据：时间复杂度为 $O(N)$, $N$ 为数据位于链表的位置。
    • 插入指定的数据：时间复杂度为 $O(N)$, $N$ 为数据位于链表的位置。因为插入数据之前，需要先查找到可以插入的位置。
    • 删除指定的数据：时间复杂度为 $O(N)$, $N$ 为数据位于链表的位置。因为删除数据之前，需要先查找到可以插入的位置。
  • 有序数组：
    • 查找指定的数据：如果使用二分查找，时间复杂度为 $O(logN)$, $N$ 为数据的个数。
    • 插入指定的数据：时间复杂度为 $O(N)$, 因为数组是顺序存储，插入新的数据时，我们需要向后移动指定位置后面的数据，这里 $N$ 为数据的个数。
    • 删除指定的数据：时间复杂度为 $O(N)$, 因为数组是顺序存储，删除数据时，我们需要向前移动指定位置后面的数据，这里 $N$ 为数据的个数。

而神奇的跳表能够在 $O(logN)$ 时间内完成增加、删除、搜索操作。
下面我们分别分析增加、删除和搜索这 3 个三个基本操作。

跳表的查找

现在我们通过一个简单的例子来描述跳表是如何实现的。假设我们有一个有序链表如下图：

原始方法中，查找的时间复杂度为 $O(N)$。那么如何来提高链表的查询效率呢？
如下图所示，我们可以从原始链表中每两个元素抽出来一个元素，加上一级索引，并且一级索引指向原始链表：

如果我们想要查找 9 ，在原始链表中查找路径是 1->3->4->7->9, 而在添加了一级索引的查找路径是 1->4->9，很明显，查找效率提升了。
按照这样的思路，我们在第 1 级索引上再加第 2 级索引，再加第 3 级索引，以此类推，这样在数据量非常大的时候，使得我们查找数据的时间复杂度为 $O(logN)$。这就是跳表的思想，也就是我们通常所说的“空间换时间”。

跳表的插入

跳表插入数据看起来很简单，我们需要保持数据有序，因此，第一步我们需要像查找元素一样，找到新元素应该插入的位置，然后再插入。

但是这样会存在一个问题，如果我们一直往原始链表中插入数据，但是不更新索引，那么会导致两个索引结点之间的数据非常多，在极端情况下，跳表会退化成单链表，从而导致查找效率由 $O(logN)$ 退化为 $O(N)$。因此，我们需要在插入数据的同时，增加相应的索引或者重建索引。

  1. 方案 1：每次插入数据后，将跳表的索引全部删除后重建，我们知道索引的结点个数为 $N$（在空间复杂度分析时会有明确的数学推导），那么每次重建索引，重建的时间复杂度至少是 $O(N)$ 级别，很明显不可取。
  2. 方案 2：通过随机性来维护索引。假设跳表的每一层的提升概率为 $\frac{1}{2}$ ，最理想的情况就是每两个元素提升一个元素做索引。而通常意义上，只要元素的数量足够多，且抽取足够随机的话，我们得到的索引将会是比较均匀的。尽管不是每两个抽取一个，但是对于查找效率来讲，影响并不很大。我们要知道，设计良好的数据结构往往都是用来应对大数据量的场景的。
    因此，我们这样维护索引：随机抽取 $\frac{N}{2}$ 个元素作为 1 级索引，随机抽取 $\frac{N}{4}$ 作为 2 级索引，以此类推，一直到最顶层索引。

那么具体代码该如何实现，才能够让跳表在每次插入新元素时，尽量让该元素有 $\frac{1}{2}$ 的概率建立一级索引、$\frac{1}{4}$ 的概率建立二级索引、$\frac{1}{8}$ 的概率建立三级索引，以此类推。因此，我们需要一个概率算法。

在通常的跳表实现当中，我们会设计一个 randomLevel() 方法，该方法会随机生成 1~MAX_LEVEL 之间的数 (MAX_LEVEL 表示索引的最高层数）

  • randomLevel() 方法返回 1 表示当前插入的元素不需要建立索引，只需要存储数据到原始链表即可（概率 1/2）
  • randomLevel() 方法返回 2 表示当前插入的元素需要建立一级索引（概率 1/4）
  • randomLevel() 方法返回 3 表示当前插入的元素需要建立二级索引（概率 1/8）
  • randomLevel() 方法返回 4 表示当前插入的元素需要建立三级索引（概率 1/16）
  • ……

可能有的同学会有疑问，我们需要一级索引中元素的个数时原始链表的一半，但是我们 randomLevel() 方法返回 2（建立一级索引）的概率是 $\frac{1}{4}$, 这样是不是有问题呢？
实际上，只要randomLevel()方法返回的数大于 1，我们都会建立一级索引，而返回值为 1 的概率是 $\frac{1}{2}$。所以，建立一级索引的概率其实是$1- \frac{1}{2} = \frac{1}{2}$。同上，当 randomLevel() 方法返回值 >2 时，我们会建立二级或二级以上的索引，都会在二级索引中添加元素。而在二级索引中添加元素的概率是 $1- \frac{1}{2} - \frac{1}{4} = \frac{1}{4}$。
以此类推，我们推导出 randomLevel() 符合我们的设计要求。

下面我们通过仿照 redis zset.c 的 randomLevel 的代码：

1
2
3
4
5
6
7
8
##
# 1. SKIPLIST_P 为提升的概率，本案例中我们设置为 1/2, 如果我们想要节省空间利用效率，可以适当的降低该值，从而减少索引元素个数。在 redis 中 SKIPLIST_P 被设定为 0.25。
# 2. redis 中通过使用位运算来提升浮点数比较的效率，在本案例中被简化
def randomLevel():
    level = 1
    while random() < SKIPLIST_P and level < MAX_LEVEL:
        level += 1
    return level

跳表的删除

跳表的删除相对来讲稍微简单一些。我们在删除数据的同时，需要删除对应的索引结点。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
from typing import Optional
import random

class ListNode:
    def __init__(self, data: Optional[int] = None):
        self._data = data # 链表结点的数据域，可以为空（目的是方便创建头节点）
        self._forwards = [] # 存储各个索引层级中该结点的后驱索引结点

class Skiplist:

    _MAX_LEVEL = 16 # 允许的最大索引高度，该值根据实际需求设置

    def __init__(self):
        self._level_count = 1 # 初始化当前层级为 1
        self._head = ListNode()
        self._head._forwards = [None] * self._MAX_LEVEL

    def search(self, target: int) -> bool:
        p = self._head
        for i in range(self._level_count - 1, -1, -1): # 从最高索引层级不断搜索，如果当前层级没有，则下沉到低一级的层级
            while p._forwards[i] and p._forwards[i]._data < target:
                p = p._forwards[i]

        if p._forwards[0] and p._forwards[0]._data == target:
            return True

        return False

    def add(self, num: int) -> None:
        level = self._random_level() # 随机生成索引层级
        if self._level_count < level: # 如果当前层级小于 level, 则更新当前最高层级
            self._level_count = level
        new_node = ListNode(num) # 生成新结点
        new_node._forwards = [None] * level
        update = [self._head] * self._level_count # 用来保存各个索引层级插入的位置，也就是新结点的前驱结点

        p = self._head
        for i in range(self._level_count - 1, -1, -1): # 整段代码获取新插入结点在各个索引层级的前驱节点，需要注意的是这里是使用的当前最高层级来循环。
            while p._forwards[i] and p._forwards[i]._data < num:
                p = p._forwards[i]

            update[i] = p

        for i in range(level): # 更新需要更新的各个索引层级
            new_node._forwards[i] = update[i]._forwards[i]
            update[i]._forwards[i] = new_node

    def erase(self, num: int) -> bool:
        update = [None] * self._level_count
        p = self._head
        for i in range(self._level_count - 1, -1, -1):
            while p._forwards[i] and p._forwards[i]._data < num:
                p = p._forwards[i]
            update[i] = p

        if p._forwards[0] and p._forwards[0]._data == num:
            for i in range(self._level_count - 1, -1, -1):
                if update[i]._forwards[i] and update[i]._forwards[i]._data == num:
                    update[i]._forwards[i] = update[i]._forwards[i]._forwards[i]
            return True

        while self._level_count > 1 and not self._head._forwards[self._level_count]:
            self._level_count -= 1

        return False

    def _random_level(self, p: float = 0.5) -> int:
        level = 1
        while random.random() < p and level < self._MAX_LEVEL:
            level += 1
        return level

复杂度分析

空间复杂度

跳表通过建立索引提高查找的效率，是典型的“空间换时间”的思想，那么空间复杂度到底是多少呢？
我们假设原始链表有 $N$ 个元素，一级索引有 $\frac{N}{2}$，二级索引有 $\frac{N}{4}$，k 级索引有 $\frac{N}{2^k}$ 个元素，而最高级索引一般有 $2$ 个元素。所以，索引结点的总和是 $\frac{N}{2} + \frac{N}{2^2} + \frac{N}{2^3}+…+ 2 \approx N-2$ ，因此可以得出空间复杂度是 $O(N)$, $N$ 是原始链表的长度。

上面的假设前提是每两个结点抽出一个结点到上层索引。那么如果我们每三个结点抽出一个结点到上层索引，那么索引总和就是 $\frac{N}{3} + \frac{N}{3^2} + \frac{N}{3^3} + 9 + 3 + 1 \approx \frac{N}{2}$, 额外空间减少了一半。因此我们可以通过减少索引的数量来减少空间复杂度，但是相应的会带来查找效率一定的下降。而具体这个阈值该如何选择，则要看具体的应用场景。

另外需要注意的是，在实际的应用当中，索引结点往往不需要存储完整的对象，只需要存储对象的 key 和对应的指针即可。因此当对象比索引结点占用空间大很多时，索引结点所占的额外空间（相对原始数据来讲）又可以忽略不计了。

时间复杂度

查找的时间复杂度

来看看时间复杂度 $O(logN)$ 是如何推导出来的，首先我们看下图：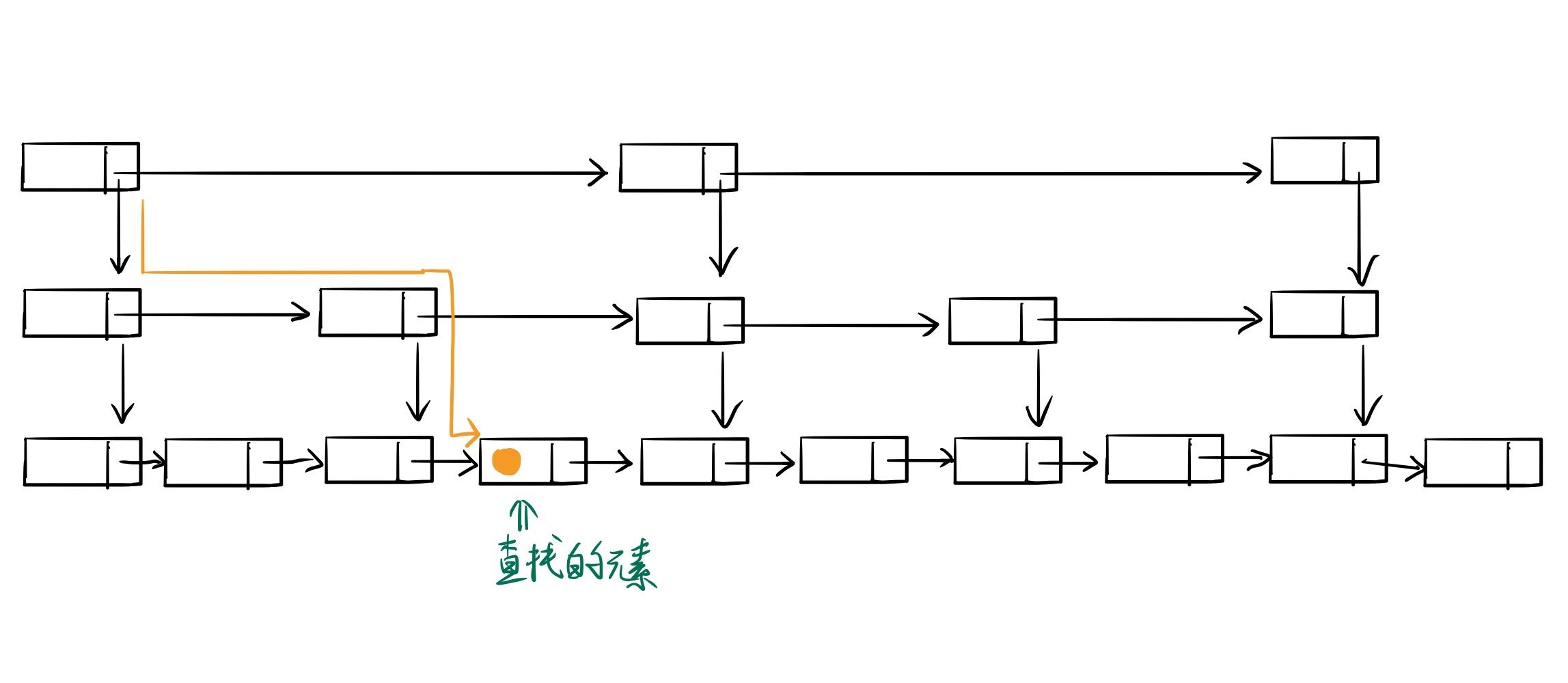

如上图所示，此处我们假设每两个结点会抽出一个结点来作为上一级索引的结点。也就是说，原始链表有 $N$ 个元素，一级索引有 $\frac{N}{2}$，二级索引有 $\frac{N}{4}$，k 级索引有 $\frac{N}{2^k}$ 个元素，而最高级索引一般有 $2$ 个元素。 也就是说：最高级索引 $x$ 满足 $2 = N/2^x$, 由此公式可以得出 $x = \log_2(N)-1$ , 加上原始数据这一层， 跳表的总高度为 $h = \log_2(N)$。
那么，我们在查找过程中每一层索引最多遍历几个元素呢？从图中我们可以看出来每一层最多需要遍历 3 个结点。
因此，由公式 时间复杂度 = 索引高度*每层索引遍历元素个数， 可以得出跳表中查找一个元素的时间复杂度为 $O(3 \times \log(N))$，省略常数即为 $O(\log(N))$。

插入的时间复杂度

跳表的插入分为两部分操作：

  1. 寻找到对应的位置，时间复杂度为 $O(logN)$, $N$ 为链表长度。
  2. 插入数据。我们在前面已经推导出跳表索引的高度为 $logN$。 因此，我们将数据插入到各层索引中的最坏时间复杂度为 $O(logN)$。

综上所述，插入操作的时间复杂度为 $O(logN)$

删除的时间复杂度

跳表的删除操作和查找类似，只是需要在查找后删除对应的元素。查找操作的时间复杂度是 $logN$。那么后面删除部分代码的时间复杂度是多少呢？我们知道在跳表中，每一层索引都是一个有序的单链表，而删除单个元素的复杂度为 $O(1)$, 索引层数为 $logN$，因此删除部分代码的时间复杂度为$logN$。那么删除操作的总时间复杂度为- $O(logN) + O(logN) = 2O(logN)$。我们忽略常数部分，删除元素的时间复杂度为 $O(logN)$。

扩展

在工业上，使用跳表的场景很多，下面做些简单的介绍，有兴趣的可以深入了解：

  1. redis 当中 zset 使用了跳表
  2. HBase MemStore 当中使用了跳表
  3. LevelDB 和 RocksDB 都是 LSM Tree 结构的数据库，内部的 MemTable 当中都使用了跳表

配套网站

官网开辟了一个区域，大家可以直接访问查看本书配套的配套代码，包括 JavaScript，Java，Python 和 C++。 也欢迎大家留言给我们自己想要支持的语言，我们会郑重考虑大家的意见。

效果大概是这样的：

实体版购书链接

电子版购书链接


 上一页

秋招

 评论


博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本站使用 Material X 作为主题 。
载入天数...载入时分秒...