这个我为自己的新书写的一个目录,计划在一星期左右定下来大体目录,然后投入完善,希望大家多提意见,你的意见很可能会影响到这本书的内容,期待你以特别的方式参与进来,此致敬礼。
1. 准备知识
1.1 学习这本书之前需要什么基础
很多人觉得算法很难,需要很多公式以及数学知识。 其实并不是这样的,除非你是做算法岗位,否则并不会要求你对数学,几何学,概率学有多深的造诣,其实更看重的是分析问题,解决问题的能力和基础编码能力。
但是我们不排除 LeetCode 有一些数学题目,我们会在后面的章节中讲到,但是说实话 LeetCode 的数学题目不会涉及很难的数学知识。而且通常我们也可以通过变通的方式解决,比如 LeetCode 有一道水壶倒水的问题,以下是题目描述:
1 | 给你一个装满水的 8 升满壶和两个分别是 5 升、3 升的空壶,请想个优雅的办法,使得其中一个水壶恰好装 4 升水,每一步的操作只能是倒空或倒满。 |
这道题我们可以用 GCD(最大公约数)解决,如果你不知道这个数学知识点也没问题。 我们可以通过 BFS 来解决,其实学习算法尤其是刷 LeetCode 只需要我们掌握简单的数学知识,高中的数学知识通常来说就足够了。
另外一个大家需要掌握的数学知识是关于后面要讲的复杂度分析,这里需要一点简单的数学知识,不过不要担心,非常简单,不会有高等数学的内容。
学习本书最好你对一种编程语言比较熟悉,出于读者的受众群体和代码简洁性,我选取了 Python 作为本书的主要编程语言,如果大家对 Python 不熟悉也没有关系,我会尽量少使用语言特有的语法糖,从而减少大家对于语言层面的认知负担。 另外 Python 被誉为最容易入门的语言之一也是实至名归,大家可以放心。 退一步讲,语言不应该成为我们学习算法的障碍,不是么?那让我们一起进入 LeetCode 的世界吧!
1.2 基础数据结构和算法
在真正的刷题之前,我们一定要先打好基础,学好基本的数据结构和算法,然后以练代学进行提升和消化。
从广义上来说,数据结构其实就是数据的存储结构,算法就是操作数据的方法。而平时以及本书所探讨的其实是更为狭义角度的数据结构和算法。其实指的是某些非常典型的数据结构和算法,比如数组,链表,栈,队列,树,图等数据结构,以及二分法,动态规划,快速排序等经典的算法。
数据结构是为算法所服务的,而算法是要建立在某一种或者几种数据结构之上才可以发挥作用,这两个是相辅相成的关系。某些算法一定要建立在某种数据结构之上才行,相信你读完这本书会对这句话产生更为深刻的印象。
本书要讲的内容就是在 LeetCode 上反复出现的算法,经过进一步提炼,抽取近百道题目在这里进行讲解,帮助大家理清整体结构,从而高效率地刷题。
我这里总结了 7 个常见的数据结构和 7 个常见的算法以及 5 个常见的算法思想。
7 个数据结构分别是: 数组,栈,队列,链表,二叉树,散列表,图
7 个算法分别是:二分法,递归,回溯法,排序,双指针,滑动窗口,并查集
5 个算法思想分别是:分治,贪心,深度优先遍历,广度优先遍历,动态规划
只有掌握了这些基础的数据结构和算法,更为复杂的算法才能得心应手,刷题才会事半功倍。而 LeetCode 的题目虽然不断出新,但是最终用到的算法永远是那几个,很多题目都是穿着新衣服的老面孔了。大家学好这些基础套路之后会更加明白这个道理。
1.3 如何刷 LeetCode
Leetcode 网站使用方法
LeetCode 官网收录了许多互联网公司的算法题目,一度被称为刷题神器,今天我们就来介绍下如何使用 LeetCode 网站,以下所讲述的内容都是以力扣中国为例。
LeetCode 目前有 1000 多道题目,并且一直持续更新,其中有一些是带锁的,需要会员才能查看。 最上面标签栏的 Problems,给出了四个分类:Algorithms、Database、Shell 和 Concurrency,分别表示算法题、数据库题、Shell 和并发题,第一个就是我们所需要刷的算法题,并发是 2019 年才添加的新的模块。
点开 Algorithms 后,我们可以看到一列题目的列表,每个题目都有一个序号,后面的接受率(Acceptance)表示提交的正确率,Difficulty 表示难易程度。这里有个小技巧,衡量一道题目难不难除了看难度之外,还可以看下接受率,接受率越低代表题目越难,这个指标有时候比难度更靠谱。
LeetCode 按难易程度分成了三个级别,分别是 Easy、Medium 和 Hard。
- Easy 通常不需要太多思考和也不会有复杂的细节,比较特别适合新手或者拿来热身。
- Medium 级别就会有些难度,一般都会涉及到经典的算法,需要一定的思考。
- Hard 级别是最难的,有些时候是算法本身的难度,有些时候特别需要你考虑到各种细节。
你可以对题目进行筛选和排序。
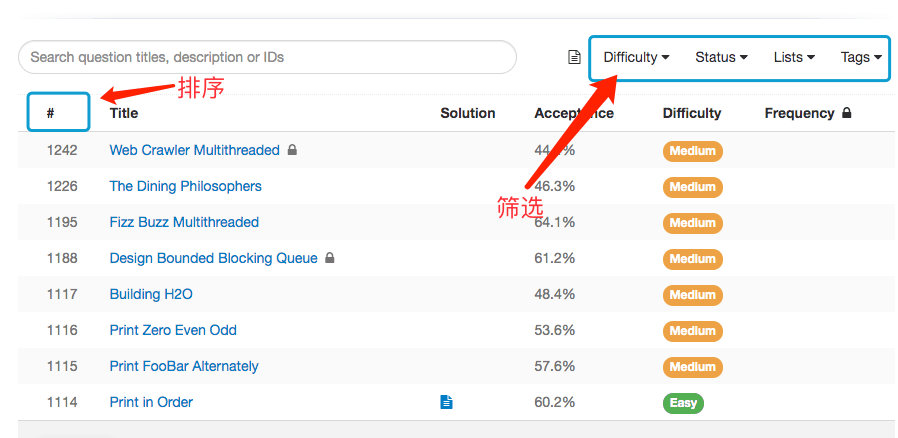
如果我们只想要找某一类型的题,可以通过 Tags 或 Company 来筛选。
另外我们在做某一题时,觉得还想再做一个类似的,可以点击题目描述下方 Show Similar Problems 或 Tags 来找到相似的问题。
每个题目都有各自的 Discuss 区域。在这里,许多人都把自己的思路和代码放到了上面,你可以发贴提问,也可以回复别人,里面大神很多,题解质量都很高,如果实在没有思路或者想看下有没有更好的思路可以来逛一下。通常来说我建议你优先看 Post 或者投票最多的。
点开某一个题目,会跳转到具体题目详情页面,你可以在右侧的代码区切换选择自己需要的编程语言。
代码编写完了之后,不要急着提交,先可以测试运行下(Run Code),你可以多写几个测试用力跑一下,没有问题再提交,要知道比赛的时候错误提交要加时间的。 我们可以点开 More Details 查看详细运行结果信息。
每道题旁边的 My Submissions 可以找到自己的对于该题的提交情况,这里可以看到自己过去所有的提交,点 Accepted 或 Wrong Answer 就可以查看自己过去提交的代码情况,包括代码是什么,跑的时间以及时间分布图等。
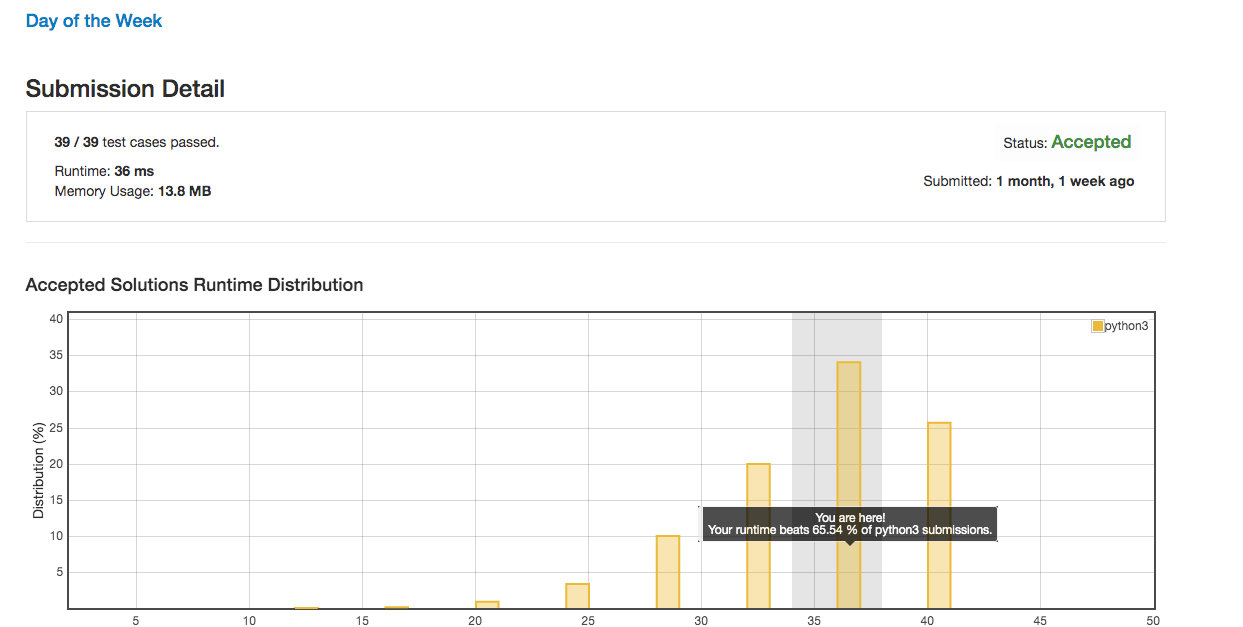
以上就是 LeetCode 的主要功能,希望通过这一节内容能让你对 LeetCode 网站有所了解,从而更快地进行刷题。
应该怎么刷 LeetCode
我本人从开始准备算法以来刷了很多题,自己成长了很多,从刷题菜鸡,到现在对刷题套路,题型有了自己的理解,感受还是蛮多的。我本人不是算法高手,算是勤能补拙类型。不过经过几个月的学习和练习,不仅面试变得更加得心应手,而且在工作中写更容易写出干净优雅,性能好的代码。
对于我来说,刷题的过程其实就是学习数据结构和算法的过程, 不仅仅是为了刷题而刷题,这样你才能感受到刷题的乐趣。刷题至少要刷两遍,理想情况是根据自己的遗忘曲线刷多次,这个我后面也会讲到。
- 第一遍按 tag 刷
建议第一遍刷的时候可以先快速按照 tag 过一遍,快速感受一下常见数据结构和算法的套路,这样自己有一个感性的认识。
- 第二遍一题多解,多题同解
第二遍我们就不能像第一遍那样了,这个阶段我们需要多个角度思考问题,尽量做到一题多解,多题同解。我们需要对问题的本质做一些深度的理解,将来碰到类似的问题我们才能够触类旁通。
但是很多人做了几遍,碰到新题还是没有任何头绪,这是一个常见的问题,这怎么办呢?
总结并记忆是学习以及刷题过程中非常重要的一环, 不管哪个阶段,我们都需要做对应的总结,这样将来我们再回过头看的时候,才能够快读拾起来。
anki 就是根据艾宾浩斯记忆曲线开发的一个软件,它是一个使记忆变得更容易的学习软件。支持深度自定义。 对于我本人而言,我在 anki 里面写了很多 LeetCode 题目和套路的 Card,然后 anki 会自动帮我安排复习时间,大大减少我的认知负担,提高了我的复习效率。大家可以在书后的附录中下载 anki 卡片。
目前已更新卡片一览(仅列举正面)
- 二分法解决问题的关键点是什么,相关问题有哪些?
- 如何用栈的特点来简化操作, 涉及到的题目有哪些?
- 双指针问题的思路以及相关题目有哪些?
- 滑动窗口问题的思路以及相关题目有哪些?
- 回溯法解题的思路以及相关题目有哪些?
- 数论解决问题的关键点是什么,相关问题有哪些?
- 位运算解决问题的关键点是什么,相关问题有哪些?
大家刷了很多题之后,就会发现来来回回,题目就那么几种类型,因此掌握已有题目类型是多么重要。那样 LeetCode 出题的老师,很多也是在原有的题目基础上做了适当扩展(比如 two-sum,two-sum2,three-sum, four-sum 等等)或者改造(使得不那么一下子看出问题的本质,比如猴子吃香蕉问题)。
其中算法,主要是以下几种:
1 | 基础技巧:分治、二分、贪心 |
数据结构,主要有如下几种:
1 | 数组与链表:单 / 双向链表 |
做到了以上几点,我们还需要坚持。这个其实是最难的,不管做什么事情,坚持都是最重要也是最难的。
为了督促自己,同时帮助大家成长,我在群里举办《每日一题》活动,每日一题是在交流群(包括微信和 qq)里进行的一种活动,大家一起 解一道题,这样讨论问题更加集中,会得到更多的反馈。而且 这些题目可以被记录下来,日后会进行筛选添加到仓库的题解模块, 感兴趣的可以到书后的附录部分进群交流。
1.4 复杂度分析
想学算法,首先要学的第一件事就是如何判断一个算法的好坏。 好的程序有很多的评判标准,包括但不限于可读性,扩展性性能等。 这里我们来看其中一种 - 性能。 坏的程序可能性能也很好,但是好的程序通常性能都比较好。那么如何分析一个算法的性能好坏呢?这就是我们要讲的复杂度分析,所有的数据结构教程都会把这个放在前面来讲,不仅仅是因为他们是基础,更因为他们真的非常重要。学会了复杂度分析,你才能够对你的算法进行分析,从而帮助你写出复杂度更优的算法。
那么怎么样才能衡量一个算法代码的执行效率呢?
如下是一个从 1 加到 n 的一个算法,这个算法用了一层循环来完成,并且借助了一个变量 res 来完成。
1 | def sum(n): |
我们将这个方法从更微观的角度来进行分析,上述代码会执行 n 次循环体的内容,每一次执行都是常数时间,我们不妨假设执行的时间是 x。我们假设赋值语句res = 0和return res的时间分别为 y 和 z 那么执行的总时间我们约等于 n _ x + y + z, 我们粗略将 x,y 和 z 都看成一样的,我们得出总时间为 (n + 2) _ x 换句话说算法的时间和数据的规模成正比。
实际上,这更是一种叫做大 O 表示法的基本思想, 它是一种描述算法性能的记法,这种描述和编译系统、机器结构、处理器的快慢等因素无关。 这种描述的参数是 n,表示数据的规模。 这里的 O 表示量级(order),比如说“二分查找是$O(logN)$的”,也就是说它需要“通过 logn 量级的操作去查找一个规模为 n 的数据结构(通常是数组)”。这种渐进地估计对算法的理论分析和大致比较是非常有价值,可以很快地对算法进行一个大致地估算。例如,一个拥有较小常数项的 $O(N^2)$算法在规模 n 较小的情况下可能比一个高常数项的$O(N)$算法运行得更快。但是随着 n 足够大以后,具有较慢上升函数的算法必然工作得更快,因此在采用大 O 标记复杂度的时候,可以忽略系数。
我们还应该区分算法的最好情况,最坏情况和平均情况,但是这不在本书的讨论范畴,本书的所有复杂度均指的是平均复杂度。
那么如何分析一个算法的复杂度呢?下面我们介绍几种常见时间复杂度,几乎所有的算法的复杂度都是以下中的一种
我对时间复杂度进行了一个小的分类。
- 第一类是常数阶。
一般情况下,只要算法中不存在循环语句、递归语句,即使有成千上万行的代码,其时间复杂度也是 Ο(1)。
1 | cnt = 1 |
- 第二类是 n,n^2,n^3 …
一个简单的方法是关注循环执行次数最多的那一段代码就好了,这段执行次数最多的代码执行次数的 n 的量级,就是整个算法的时间复杂度。即如果是一层 N 的循环,那么时间复杂度就是$O(N)$, 如果嵌套了两层 N 的循环,那么时间复杂度就是$O(N^2)$,依次类推。
1 |
|
如上代码,我们进行了一层的循环,那么时间复杂度就是$O(N^2)$
- 第三类是对数阶。 logn nlogn
这同样是一种非常常见的复杂度,多见于二分查找和一些排序算法。
1 | def numRescueBoats(self, people: List[int], limit: int) -> int: |
上面的代码是一个典型的二分查找,其时间复杂度是 logn
- 第四类是指数阶 2^n
指数的增长已经非常恐怖了,一个典型的例子是 fabnicca 数列的递归实现版本。
1 | def fibonacci(n): |
如果你把上述的计算过程看成树的一个节点,那么整个计算过程就像是一颗很大的树。这棵树有很多的重复计算,大致算下来的话,是 2^n。
- 第五类是对数阶 n!
我们知道 n 个不相同的数字的全排列有 n!个。
1 | def factorrail(n): |
很明显上面的代码就是 n!
下面给出上面列举的几种常见的时间复杂度的趋势图对比,大家直观感受一下。
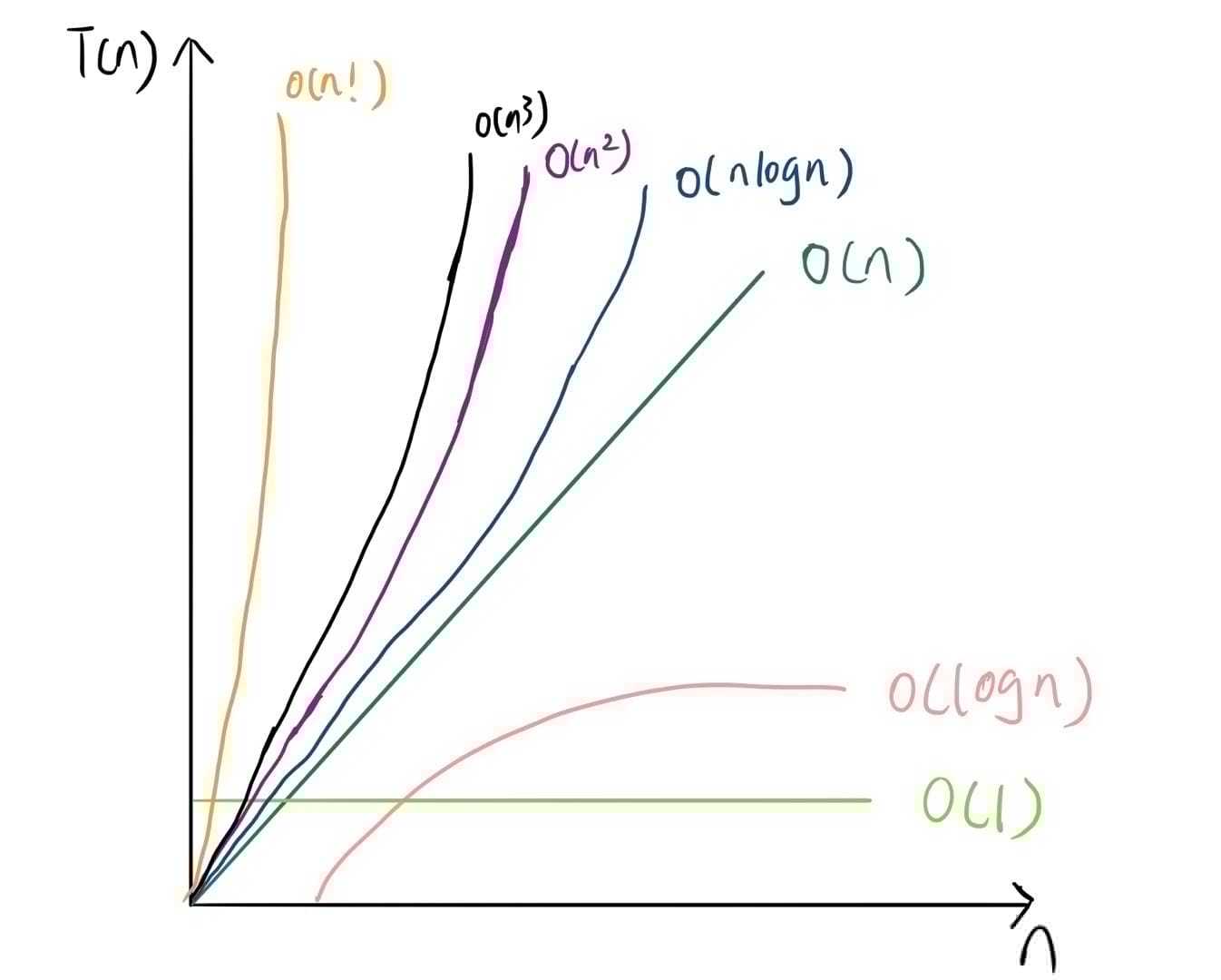
(各种复杂度的渐进趋势对比)
从算法可以分析出时间复杂度,相反题目的时间复杂度要求,我们甚至可以猜测出可能用到的算法,比如算法要求 logn,那么就有可能是二分法。
空间复杂度分析比时间复杂度分析要简单地多,常见的空间复杂度有$O(1)$、$O(N)$、$O(N^2)$、$O(logN)$、$O(logN)$、$O(N!)$这样的对数阶复杂度基本不会有,关于空间复杂度这里不做更多介绍了。
总结
时间复杂度是算法的基石,学习它对于我们学习后面的章节有很大的帮助。 我们引入了大 O 表示法来衡量算法的好坏。接着通过若干实例了解了各种时间复杂度,其实对于复杂度,掌握上面提到的几种常见的就已经够应付绝大多数场合了。
通过上面的学习,相信你对评估一个算法的时间复杂度有了初步的了解。随着学习的深入,相信你会对复杂度分析有着更为深入的理解。
2. 数学之美
LeetCode 中有很多数学问题,截止到本书出版,LeetCode 中有数学标签的题目一共是 159,在所有标签的分类中排名第 3。这些题目中有些是包着数学外衣的伪数学问题,还有一些是真正数学问题。这需要大家有着极强的分辨能力。不要被数学两个字吓住了,本章不会讲非常复杂的数学概念和公式,实际上你只需要一些高中数学知识即可。
除非是面试算法岗位,笔试和面试题才会涉及到一些比较复杂度的数学知识,比如微积分,线性代数,概率论,信息论等。
虽然有的题目可以用数学公式轻松解决,但是这并不意味你需要对数学有很深的造诣。举例来说,LeetCode 69.实现开方,就是一道可以使用纯数学方法 - 牛顿迭代法来解决的一道题,但是你完全可以使用二分法解决,尽管效率远远不及牛顿迭代法,实际上现在的计算器计算开方也不是二分法计算的。但是这通常是一个加分项,如果你可以通过别的方法解决,也未尝不可。
很多题目一眼看上去就是个数学问题,如果你尝试使用数学的角度没有什么思路或者解不出来的时候,可以考虑换最常规,最符合直觉的做法,当然做之前要估算一下数据范围和时间,不要写完才发现超时。
有些题目只是涉及到一些数学名词,并且会在题目中详细地进行解释。 比如关于质数性质,阶乘性质的题目,还有一些造轮子题目,比如实现 Pow 等。还有一些干脆定义一个数学概念,让你去做。比如开心数,回文数,丑数等。
我们这章主要讲解纯数学问题,需要用到一些数学的性质类的题目,这或许是大家更想要看的。
2.1 N-SUM 题目
LeetCode 上有很多经典的系列问题,今天我们就来看一下 N-SUM 系列问题。
2.2 连续整数和
这是一个非常经典,被各种收录的一个题目,这道题好在虽然简单,但是却可以从多个纬度进行解决,非常适合用来查考一个人的真实水平,一些比较大的公司也会用它来进行算法面试的第一道题。
2.3 最大数
2.4 分数到小数
2.5 最大整除子集
2.6 质数排列
质数
全排列
2.8 快乐数
这类题目是给定一个定义(情景),让你实现算法找出满足特定条件的数字
3. 回文的艺术
回文是很多教材中被提到的一个题目,通常是用来学习栈的一个练习题,LeetCode 中有关回文的题目也是蛮多的,单从数据结构上来看就有字符串,数字和链表。今天我们就结合几个 LeetCode 题目来攻克它。
3.1 回文字符串
3.2 回文链表
3.3 回文数字
3.4 回文总数
4. 游戏之乐
我很喜欢玩游戏,实际上很多游戏背后都是有很多算法存在的,我们通过 LeetCode 上一些关于游戏的题目来一窥究竟吧,虽然这里的题目和实际游戏用到的算法难度差很多,但是这里的基本思想是一样的。
4.1 生命游戏
4.2 报数
4.3 数独游戏
5. BFS & DFS
这是 LeetCode 后期新增的一个板块,题目还比较少。
6. 二分法
二分法真的是一个非常普遍的算法了,更严格的说其实是一种思想,如果把二改成 N 其实就是一种分治思想。LeetCode 关于二分法的题目实在太多了,我们挑选几个代表性的来感受一下,LeetCode 到底是如何考察我们二分法的。
6.1 你真的了解二分法么?
6.2 一些显然的二分
6.3 隐藏的二分法
二进制和二分法?
744 吃香蕉 循环数组 数学开方 等等
6.4 寻找峰值
7. 神奇的比特
前菜: 如何将一个 IP 地址用一个字节存储,支持序列化和反序列化操作。
计算机是用过二进制来表示信息的,有时候我们从二进制思考问题,会发现一个全新的世界。
7.1 那些特立独行的数字
7.2 桶中摸黑白球
7.3 实现加法
7.4 二进制 1 的个数
7.5 悲惨的老鼠
8. 设计题
有时候我们面对的不是一个算法题,而是一个设计题目,这种题目比较开放,让你自己设计数据结构和算法。这比限定数据结构和算法更能考察一个人综合运用知识的能力,是一个经常被拿来进行面试的一类题目。
8.1 设计 LRU
8.2 设计 LFU
8.3 最小栈
8.4 队列实现栈
8.5 设计 Trie 树
9. 双指针
双指针的题目真的非常多,可以看出这个是一个重要重要的知识点。在实际使用过程中,我将双指针问题分为两种,一种是头尾双指针,一种是快慢双指针。
9.1 头尾指针
9.1.1 盛水问题
9.1.2 两数相加 2
9.2 快慢指针
9.2.1 删除有序数组的重复元素
9.2.2 链表中的快慢指针
10. 查表与动态规划
如果说递归是从问题的结果倒推,直到问题的规模缩小到寻常。 那么动态规划就是从寻常入手, 逐步扩大规模到最优子结构。 这句话需要一定的时间来消化, 如果不理解,可以过一段时间再来看。
递归的解决问题非常符合人的直觉,代码写起来比较简单。但是我们通过分析(可以尝试画一个递归树),可以看出递归在缩小问题规模的同时可能会 重复计算。 279.perfect-squares 中 我通过递归的方式来解决这个问题,同时内部维护了一个缓存 来存储计算过的运算,那么我们可以减少很多运算。 这其实和动态规划有着异曲同工的地方。
10.1 爬楼梯
10.2 聪明的盗贼
六(七)个版本,带你一步步进化,走向极致
10.3 不同路径
10.4 硬币找零
10.5 最短编辑距离
11. 滑动窗口
你可能听过 TCP 的滑动窗口,这里要讲的滑动窗口其实思想是一样的,这里要讲的滑动窗口通常被用在处理连续数组或者字符的问题上。
最长连续不重复子串
最短子数组之和
滑动窗口最大值
12. 博弈
博弈,词语解释是局戏、围棋、赌博。 现代数学中有博弈论,亦名“对策论”、“赛局理论”,属应用数学的一个分支, 表示在多决策主体之间行为具有相互作用时,各主体根据所掌握信息及对自身能力的认知,做出有利于自己的决策的一种行为理论。
这类问题通常没那么直接和好下手,需要你进行一定的推演才能发现问题的本质。
12.1 alec
12.2 Nim
12.3 486. 预测赢家
13. 股票系列
LeetCode 上有很多经典的系列问题,今天我们就来看一下这个股票系列问题。
13.1 股票买卖的最佳时机 1
13.2 股票买卖的最佳时机 2
13.3 股票买卖的最佳时机 3
13.4 股票买卖的最佳时机 4
14. 分治法
分治是一种非常重要的算法思想,而不是一个算法。和具体算法不同,算法思想在任何数据结构下都可以使用。
14.1 合并 K 个排序链表
14.2 数组中的第 K 个最大元素
14.3 搜索二维矩阵
15. 贪心法
贪心或许是最难的一种算法思想了。
15.1 跳跃游戏
15.2 任务调度器
16. 回溯
这是一种非常暴力的搜索算法,优点是书写简单有固定模板,且适用范围很广。
16.1 求组合数 1
16.2 求组合数 2
16.3 求所有子集
16.4 全排列
16.5 海岛问题
17. 一些有趣的题目
这里让我们来看一下 LeetCode 上那些惊人的算法。
17.1 求众数
17.2 手撕排序
17.3 星期几
17.4 量筒问题
17.5 实现开方
17.6 4 的次方
18. 一些通用解题模板
不仅是平时做工程项目,刷题的过程也非常讲究风格一致,如果有一些非常优秀的模板可以直接拿来用,一方便减少做题时间和出错的可能,另一方面做题风格一致有利于自己回顾。 如果你是在面试,相信一定也会为你加分不少。
18.1 二分法
18.2 回溯法
18.3 递归
18.4 并查集
- 朋友圈
- 计算小岛数 2
19. 融会贯通
这里我们要把本书降到的知识进行融会贯通,纵向上我们不满足于一种解法,我们尝试使用多种解法去解决。 横向上我们需要去总结哪些题目和这道题目类似。
这通常被用在第二遍刷 LeetCode 的过程中。
19.1 最大子序列和问题
19.2 循环移位问题
19.3 k 问题
20. 解题技巧&面试技巧
在水平知识一样的情况下,如果能够 LeetCode 上效率更好?如何面试的时候加分,这是本章我们要探讨的主要内容。
- 一定要看限制条件,很多时候限制条件起到了提示的作用,并且可以帮助你过滤错误答案



