Floyd-Warshall 是解决任意两点间的最短路径的一种算法,LeetCode 有很多题目都用了,掌握这套解题模板帮你快速 AC。
题目地址(1334. 阈值距离内邻居最少的城市)
题目描述
1 | 有 n 个城市,按从 0 到 n-1 编号。给你一个边数组 edges,其中 edges[i] = [fromi, toi, weighti] 代表 fromi 和 toi 两个城市之间的双向加权边,距离阈值是一个整数 distanceThreshold。 |
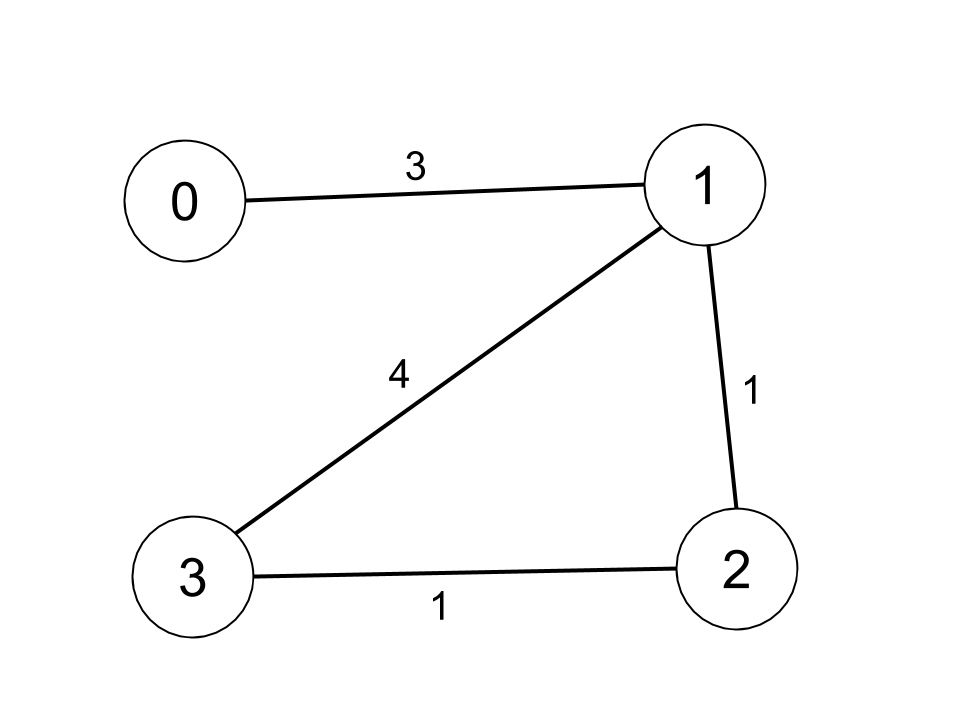
1 |
|
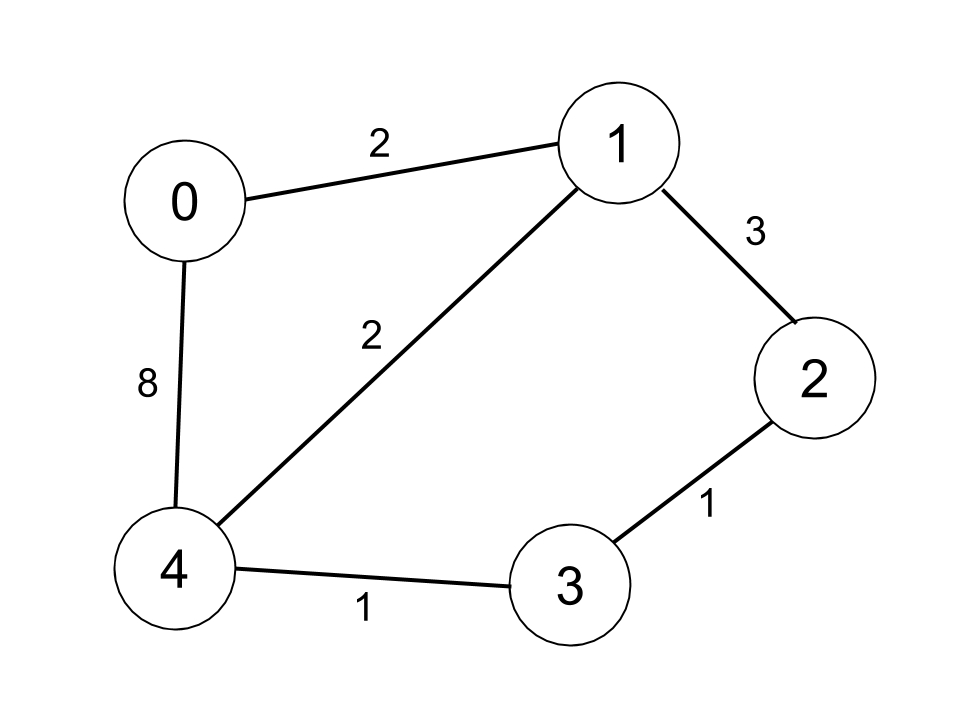
1 |
|
思路
这道题的本质就是:
- 在一个无向图中寻找每两个城镇的最小距离,我们使用 Floyd-Warshall 算法(英语:Floyd-Warshall algorithm),中文亦称弗洛伊德算法,是解决任意两点间的最短路径的一种算法。
- 筛选最小距离不大于 distanceThreshold 的城镇。
- 统计每个城镇,其满足条件的城镇有多少个
- 我们找出最少的即可
Floyd-Warshall 算法的时间复杂度和空间复杂度都是$O(N^3)$, 而空间复杂度可以优化到$O(N^2)$。Floyd-Warshall 的基本思想是对于每两个点之间的最小距离,要么经过中间节点 k,要么不经过,我们取两者的最小值,这是一种动态规划思想,详细的解法可以参考Floyd-Warshall 算法(wikipedia)
代码
代码支持:Python3
Python3 Code:
1 | class Solution: |
关键点解析
- Floyd-Warshall 算法
- 你可以将本文给的 Floyd-Warshall 算法当成一种解题模板使用



