文科生都能看懂的循环移位算法

循环移位问题真的是一个特别经典的问题了，今天我们就来攻克它。

循环移位的表现形式有很多种，就数据结构来说包括数组，字符串，链表等。就算法来说，有包含问题，直接移动问题，还有查找问题等。

虽然表现形式有很多，但是本质都是一样的，因为从逻辑上来讲其实他们都是线性数据结构，那么让我们来看一下吧。

数组循环移位

LeetCode 和 编程之美等都有这道题目，题目难度为 Easy。LeeCode 链接

题目描述

给定一个数组，将数组中的元素向右移动 k 个位置，其中 k 是非负数。

示例 1:

输入: [1,2,3,4,5,6,7] 和 k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右旋转 1 步: [7,1,2,3,4,5,6]
向右旋转 2 步: [6,7,1,2,3,4,5]
向右旋转 3 步: [5,6,7,1,2,3,4]
示例 2:

输入: [-1,-100,3,99] 和 k = 2
输出: [3,99,-1,-100]
解释:
向右旋转 1 步: [99,-1,-100,3]
向右旋转 2 步: [3,99,-1,-100]
说明:

尽可能想出更多的解决方案，至少有三种不同的方法可以解决这个问题。
要求使用空间复杂度为 O(1) 的 原地 算法。

不符合题意的解法

如果你拿到这道题没有思路，不要紧张，因为你不是一个人。

让我们先不要管题目的时间和空间复杂度的限制， 来用最最普通的方式实现它，看能不能得出一点思路。

最简单的做法就是新开辟一个完全一样的数组，然后每次移动的时候从 copy 的数组中取即可，由于新开辟的数组不会被改变，因此这种做法可行，我们直接看下代码：

function RShift(list, k) {
  // 空间复杂度O(n)
  // 时间复杂度O(n)
  const copy = [...list];
  const n = list.length;

  for (let i = 0; i < n; i++) {
    list[(k + i) % n] = copy[i];
  }
  return list;
}

实际上我们还可以优化一下，如果 k 是 N 的倍数，实际上是不需要做任何移动的，因此直接返回即可。

function RShift(list, k) {
  const n = list.length;
  if (k % n === 0) return;
  // 剩下代码
}

由于我们需要覆盖原来的数组，那么原来的数组中的数据就会缺失，因此我们最简单的就是开辟一个
完全一样的数组，这样就避免了问题，但是这样的空间复杂度是 N。我们有没有办法优化这个过程呢？

而且如果 k 是负数呢？ 这其实在考察我们思考问题的严谨性。

除此之外，我们还应该思考：

• k 的范围是多少？如果很大，我的算法还有效么？
• n 的范围是多少？如果很大，我的算法还有效么?

上面两个问题的答案都是有效。 因为 k 就算再大，我们只需要求模，求模的值当成新的 k 即可。
因此 k 最大不过就是 n。 如果 n 很大，由于我们的算法是 O(N)的复杂度，也就是线性，这个复杂度还是比较理想的。

时间换空间

我们来试一下常数空间复杂度的解法，这种做法思路很简单，我们只需要每次移动一位，移动 k 次即可，移动一次的时间复杂度是 1，k 次共用一个变量即可，因此总的空间复杂度可以降低到 1。

我们来看下代码，这次我们把上面提到的 k 为负数的情况考虑进去。

function RShift(list, k) {
  const n = list.length;
  if (k % n === 0) return;

  let cnt = Math.abs(k > 0 ? k % n : n + (k % n));
  let t = null;

  while (cnt--) {
    t = list[n - 1];
    // 右移一位
    for (let i = n - 1; i > 0; i--) {
      list[i] = list[i - 1];
    }
    list[0] = t;
  }

  return list;
}

虽然上面的解法是常数空间复杂度，但是时间复杂度是 O(N * K)，K 取值不限制的话，就是 O(N^2)，
还是不满足题意。不过没关系，我们继续思考。

我们再来看一种空间换时间的做法，这种做法的思路是拼接一个完全一样的数组到当前数组的尾部，然后问题就转化为截取数组使之满足右移的效果，这样的时间复杂度 O(N),空间复杂度是 O(N).

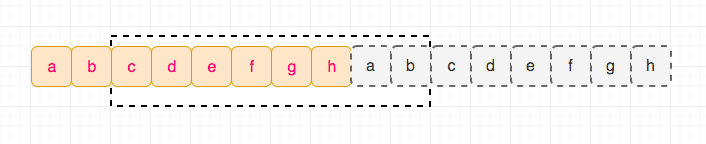
我们看下代码：

function RShift(list, k) {
  const n = list.length;
  let i = Math.abs(k > 0 ? k % n : n + (k % n));
  return list.concat([...list]).slice(n - i, n * 2 - i);
}

哈哈，虽然离题目越来越远了，但是扩展了思路，也不错，这就是刷题的乐趣。

三次翻转法

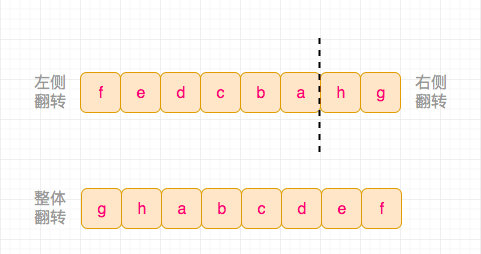
我们来看下另外一种方法 - 经典的三次翻转法，我们可以这么做：

• 先把[0, n - k - 1]翻转
• 然后把[n - k, n - 1]翻转
• 最后把[0, n - 1]翻转

function reverse(list, start, end) {
  let t = null;

  while (start < end) {
    t = list[start];
    list[start] = list[end];
    list[end] = t;
    start++;
    end--;
  }
}
function RShift(list, k) {
  const n = list.length;
  if (k % n === 0) return;
  reverse(list, 0, n - k - 1);
  reverse(list, n - k, n - 1);
  reverse(list, 0, n - 1);
  return list;
}

这里给一个简单的数学证明：

• 对于[0, n - k - 1] 部分，我们翻转一次后新的坐标 y 和之前的坐标 x 的关系可以表示为y = n - 1 - k - x
• 对于[n - k, n -1] 部分，我们翻转一次后新的坐标 y 和之前的坐标 x 的关系可以表示为y = 2 * n - 1 - k - x

• 最后我们整体进行翻转的时候，新的坐标 y 和之前的坐标 x 的关系可以表示为

  1. y = n - 1 - (n - 1 - k - x) 即 y = k + x (0 <= x <= n - k - 1)
  2. y = n - 1 - (2 * n - 1 - k - x) 即 y = k + x - n (n - k <= x <= n - 1)

正好满足我们的位移条件。

这种做法时间复杂度是 O(N)空间复杂度 O(1)，终于满足了我们的要求。

其他类似题目推荐：

• Sentence Reversal

字符串循环移位

字符串和数组真的是一模一样，因为字符串也可以看成是字符序列，因此字符串就是数组。本质上来说，它和数组循环移位题目没有任何区别， 现在让我们来通过一道题来感受下。

题目描述

给定两个字符串 s1 和 s2，要求判定 s2 是否能被 s1 循环移位得到的字符串包含。比如，给定 s1 = AABCD 和 s2 = CDAA，返回 true 。 给定 s1 = ABCD，s2 = ACBD， 则返回 false。

题目来自《编程之美》

暴力法

s1 我们每次移动一位，然后判断逐一判断以每一个位置开头的字符串是否包含 s2，如果包含则返回 true，否则继续匹配。

这种做法很暴力，时间复杂度 O(n^2)，在 n 特别大的时候不是很有效。

代码如下：

function RIncludes(s1, s2) {
  const n = s1.length;
  const m = s2.length;
  let t = null;
  let p1; // s1的指针
  let p2; // s2的指针
  for (let i = 0; i < n; i++) {
    t = s1[0];
    for (let j = 0; j < n - 1; j++) {
      s1[j] = s1[j + 1];
    }
    s1[n - 1] = t;
    p1 = 0;
    p2 = 0;
    while (p1 < n && p2 < m) {
      if (s1[p1] === s2[p2]) {
        p1++;
        p2++;
      } else break;
    }

    if (p2 === m) return true;
  }

  return false;
}

巧用模运算

另外一种方法就是上面那种空间换时间的方式，我们将两个 s1 连接到一起，然后直接双指针即可，这里不再赘述。

这种方法虽然巧妙，但是我们花费了额外的 N 的空间，能否不借助额外的空间呢？答案是可以的，我们可以假想已经存在了另外一个相同的 s1，并且我们将它连接到 s1 的末尾。注意这里是假想，实际不存在，因此空间复杂度是 O(1)。那么如何实现呢？

答案还是利用求模。

function RIncludes(s1, s2) {
  const n = s1.length;
  const m = s2.length;
  let t = null;
  let p1; // s1的指针
  let p2; // s2的指针
  for (let i = 0; i < n; i++) {
    p1 = i; // 这一行代码变了
    p2 = 0;
    while (p1 < 2 * n && p2 < m) {
      // 不需要循环移动一位了，也就是说省了一个N的循环
      if (s1[p1 % n] === s2[p2]) {
        // 这一行代码变了
        p1++;
        p2++;
      } else break;
    }

    if (p2 === m) return true;
  }

  return false;
}

至此，这道题就告一段落了，大家如果有别的方法，也欢迎在评论区留言。

链表循环移位

链表不同于前面的数组和字符串，我们来个题目感受一下。

这里出一个 LeetCode 题目，官方难度为中等难度的一个题 - 61. 旋转链表

题目描述

给定一个链表，旋转链表，将链表每个节点向右移动 k 个位置，其中 k 是非负数。

示例 1:

输入: 1->2->3->4->5->NULL, k = 2
输出: 4->5->1->2->3->NULL
解释:
向右旋转 1 步: 5->1->2->3->4->NULL
向右旋转 2 步: 4->5->1->2->3->NULL
示例 2:

输入: 0->1->2->NULL, k = 4
输出: 2->0->1->NULL
解释:
向右旋转 1 步: 2->0->1->NULL
向右旋转 2 步: 1->2->0->NULL
向右旋转 3 步: 0->1->2->NULL
向右旋转 4 步: 2->0->1->NULL

思路

其实这个思路简单，就是先找到断点，然后重新拼接链表即可。这个断点其实就是第n - k % n个节点， 其中 k 为右移的位数，n 为链表长度。这里取模的原因和上面一样，为了防止 k 过大做的无谓运算。但是这道题目限定了 k 是非负数，那么我们就不需要做这个判断了。

如图所示：

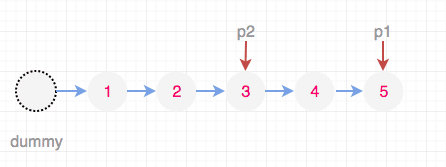
代码也很简单，我们来看下。

代码

var rotateRight = function (head, k) {
  if (head === null || head.next === null) return head;
  let p1 = head;
  let n = 1;
  let res = null;

  while (p1 && p1.next) {
    p1 = p1.next;
    n++;
  }
  let cur = 1;
  let p2 = head;

  while (cur < n - (k % n)) {
    p2 = p2.next;
    cur++;
  }
  p1.next = head;
  res = p2.next;
  p2.next = null;

  return res;
};

扩展

• 循环移位的有序数组，查找某一个值，要求时间复杂度为 O(logn)

  这道题我在《每日一题》出过