听说这题套个BFS模板就可以 AC？

​

题目描述

在一个 N × N 的方形网格中，每个单元格有两种状态：空（0）或者阻塞（1）。

一条从左上角到右下角、长度为 k 的畅通路径，由满足下述条件的单元格 C_1, C_2, ..., C_k 组成：

相邻单元格 C*i 和 C*{i+1} 在八个方向之一上连通（此时，C*i 和 C*{i+1} 不同且共享边或角）
C_1 位于 (0, 0)（即，值为 grid[0][0]）
C_k 位于 (N-1, N-1)（即，值为 grid[N-1][n-1]）
如果 C_i 位于 (r, c)，则 grid[r][c] 为空（即，grid[r][c] == 0）
返回这条从左上角到右下角的最短畅通路径的长度。如果不存在这样的路径，返回 -1 。

示例 1：

输入：[[0,1],[1,0]]

输出：2

示例 2：

输入：[[0,0,0],[1,1,0],[1,1,0]]

输出：4

提示：

1 <= grid.length == grid[0].length <= 100
grid[i][j] 为 0 或 1

思路

这道题乍一看很像之前写过的一些“机器人”。但是不同的地方在于机器人只能“向下移动和向右移动”，因此机器人那个题目就很适合用动态规划来做。为什么呢？

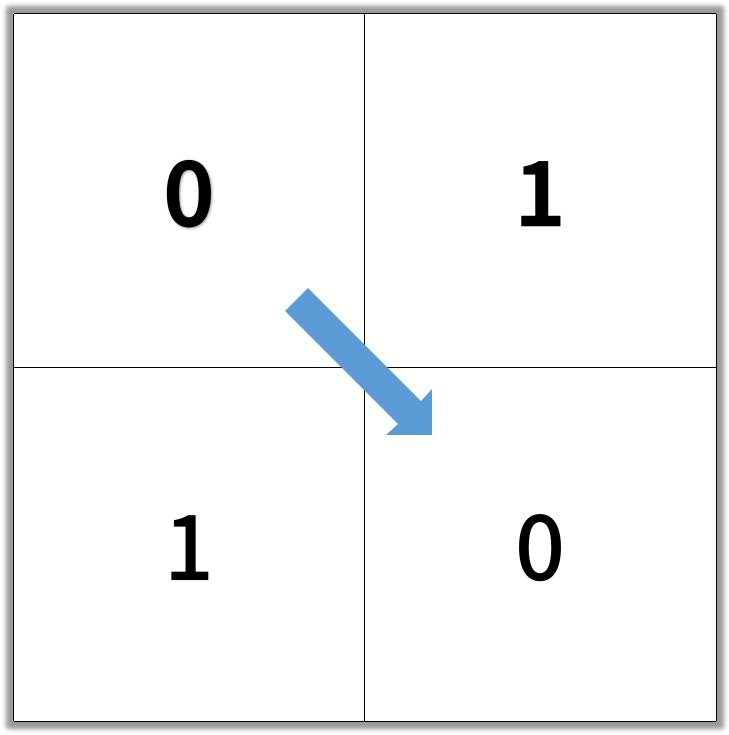
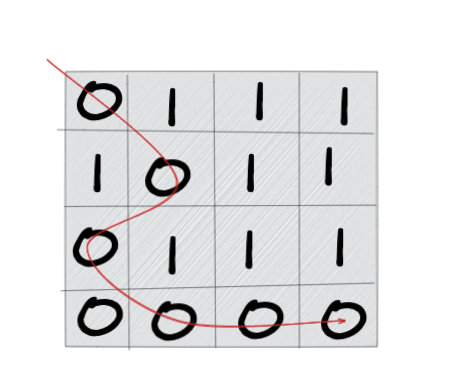
因为这道题可以移动的范围是八个方向，题目给的示例不是很好，我这里给大家画了一个示例。我相信你一看就明白了。

（图 1）

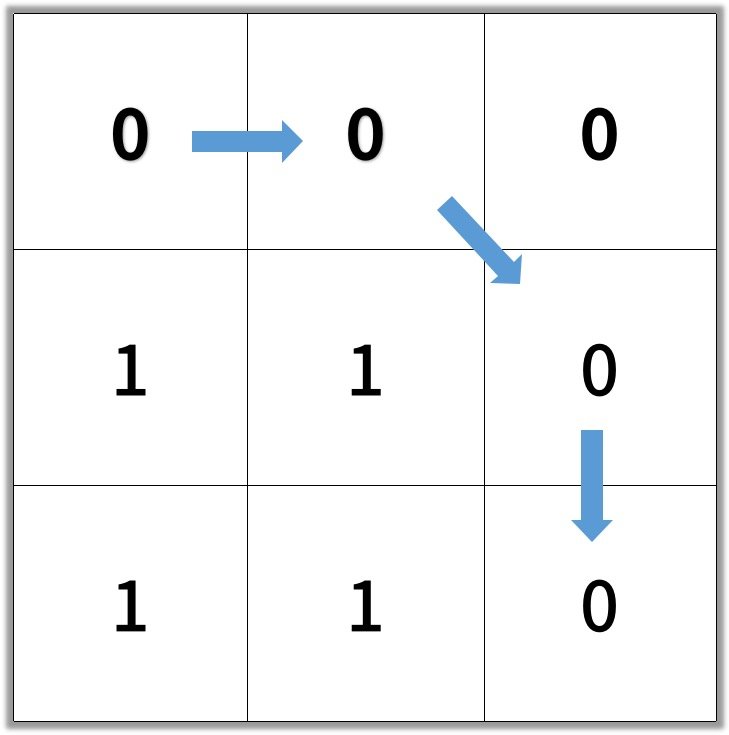
如图，我们发现每一个点的状态其实依赖了周围八个方向。如果我们使用动态规划来求解的时候，我们如何遍历（枚举所有子问题）呢？ 由于每一个 cell 依赖了周围八个 cell，那么我应该先更新谁呢？这个问题就会比较复杂。

具体来说， 当我需要计算 dp[1][2]的值的时候，实际上我需要先计算dp[0][2]，dp[1][1]，dp[2][2] … 等八个值，这样才能确定 dp[1][2]的值。而计算 dp[0][2] 又是八个值，dp[1][1]等也是同理。 这样就会很复杂。

而如果你做题比较多的话，分析到这里会发现，应该会想到 BFS。 即使你做题不多，那么根据题目给出的关键字最短畅通路径，也应该想到 BFS 才对。

这道题我直接复制了一个我直接总结的模板，稍微改了一下就 OK 了。大家也可以在平时刷题过程总结自己的解题模板，这在争分夺秒的打比赛环节是很重要的。

我复制的模板是下面这个，大家可以对比下我提交的代码看看相似度有多少。

class Solution:
    def updateMatrix(self, matrix: List[List[int]]) -> List[List[int]]:
        m = len(matrix)
        if m == 0: return []
        n = len(matrix[0])
        ans = [[0] * n for _ in range(m)]
        seen = set()
        queue = collections.deque()
        steps = 0
        for i in range(m):
            for j in range(n):
                if matrix[i][j] == 0:
                    queue.append((i, j))
                    seen.add((i, j))
        while queue:
            for _ in range(len(queue)):
                i, j = queue.popleft()
                if matrix[i][j] == 1: ans[i][j] = steps
                for x, y in [(i + 1, j), (i - 1, j),(i, j + 1),(i, j - 1)]:
                    if x >= 0 and x < m and y >=0 and y < n and (x, y) not in seen:
                        queue.append((x, y))
                        seen.add((x, y))
            steps += 1

        return ans

（Python BFS 模板代码）

我来用伪代码解释下这段代码的意思：

template BFS(board) {
  边界处理
  seen = set() # 存储已经遍历过的节点，防止环的出现。
  初始化队列
  steps = 0

  while 队列不为空 {
    逐个取出队列中的元素（不包括在 while 循环内新添加的）
    if 满足条件 return steps
    for dir in dirs {
      将周围的都加到队列，注意边界处理
    }
    steps += 1
  }

  return 不存在（一般是 -1）
}

（BFS 模板伪代码）

大家可以根据我的伪代码，自己定制属于自己的模板。

值得注意的是，本题我并没有使用 seen 来记录访问过的节点，而是直接原地修改，这是一个很常见的技巧，对这个技巧不熟悉的可以看下我的小岛专题

关键点

• BFS
• BFS 模板

代码

代码支持：Python3

class Solution:
    def shortestPathBinaryMatrix(self, grid: List[List[int]]) -> int:
        n = len(grid)
        if not grid or grid[0][0] == 1 or grid[n-1][n-1] == 1:
            return -1
        steps = 1
        queue = collections.deque()
        queue.append((0, 0))
        grid[0][0] = 1
        while queue:
            for _ in range(len(queue)):
                i, j  = queue.popleft()
                if i == n - 1 and j == n - 1: return steps
                for dx, dy in [(-1,-1), (1,0), (0,1), (-1,0), (0,-1), (1,1), (1,-1), (-1,1)]:
                    # 注意越界处理
                    if 0 <= i + dx < n and 0 <= j + dy < n and grid[i+dx][j+dy] == 0:
                        queue.append((i + dx, j + dy))
                        grid[i + dx][j + dy] = 1
            steps += 1
        return -1

复杂度分析

• 时间复杂度：最坏的情况，我们需要遍历整个 board，因此时间复杂度取决于 cell 数，故时间复杂度为 $O(N ^ 2)$，其中 N 为边长。
• 空间复杂度：我们没有使用 seen，仅仅是借助了队列， 故空间复杂度为 $O(N)$，如果使用 seen 的话复杂度会上升到$O(N ^ 2)$，其中 N 为边长。

补充：

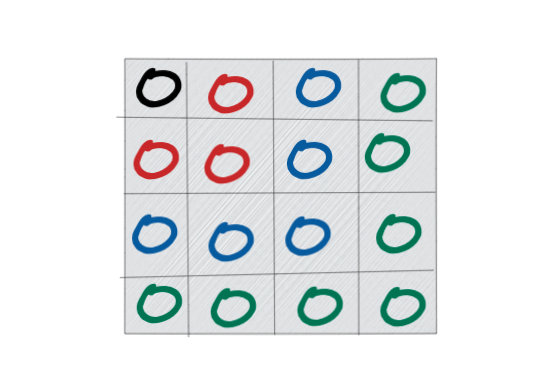
• 空间复杂度的$O(N)$ 是怎么来的？ 我这里给大家画了一个图， 相信大家一下子就懂来。其中不同的颜色表示不同的层次，从红色开始表示第一层，然后往外扩张。可以看出队列最长的情况下和$N$同阶，因此空间复杂度为$O(N)$。

相关题目

• 200. 岛屿数量
• 695. 岛屿的最大面积
• 1162. 地图分析
• 62. 不同路径

更多题解可以访问我的 LeetCode 题解仓库：https://github.com/azl397985856/leetcode 。 目前已经 30K star 啦。

大家也可以关注我的公众号《力扣加加 sa》获取更多更新鲜的 LeetCode 题解