lucifer

春招冲冲冲(网易)

lucifer

2021-03-28

春招
字数统计: 3.7k字   |   阅读时长≈ 15分

春招已经开始了。 你是不是已经开始准备了呢？为了帮助大家获得更好的 offer，lucifer 开辟了春招冲冲冲栏目。

今天我们的猎物是网易。来看看这两家的算法题难度几何吧！

​

视频地址：https://www.bilibili.com/video/BV14V411e7MF/

题目来源：https://www.nowcoder.com/discuss/625915

题目一

一组数据，判断能组成三角形最多的数，如果有多个，都写下来。

力扣原题 611. 有效三角形的个数

题目描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
给定一个包含非负整数的数组，你的任务是统计其中可以组成三角形三条边的三元组个数。

示例 1:

输入: [2,2,3,4]
输出: 3
解释:
有效的组合是:
2,3,4 (使用第一个 2)
2,3,4 (使用第二个 2)
2,2,3
注意:

数组长度不超过1000。
数组里整数的范围为 [0, 1000]。

前置知识

  • 排序
  • 双指针
  • 二分法
  • 三角形边的关系

暴力法（超时）

思路

首先要有一个数学前提： 如果三条线段中任意两条的和都大于第三边，那么这三条线段可以组成一个三角形。即给定三个线段 a，b，c，如果满足 a + b > c and a + c > b and b + c > a，则线段 a，b，c 可以构成三角形，否则不可以。

力扣中有一些题目是需要一些数学前提的，不过这些数学前提都比较简单，一般不会超过高中数学知识，并且也不会特别复杂。一般都是小学初中知识即可。

如果你在面试中碰到不知道的数学前提，可以寻求面试官提示试试。

关键点解析

  • 三角形边的关系
  • 三层循环确定三个线段

代码

代码支持: Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def is_triangle(self, a, b, c):
        if a == 0 or b == 0 or c == 0: return False
        if a + b > c and a + c > b and b + c > a: return True
        return False
    def triangleNumber(self, nums: List[int]) -> int:
        n = len(nums)
        ans = 0
        for i in range(n - 2):
            for j in range(i + 1, n - 1):
                for k in range(j + 1, n):
                    if self.is_triangle(nums[i], nums[j], nums[k]): ans += 1

        return ans

复杂度分析

  • 时间复杂度：$O(N ^ 3)$，其中 N 为 数组长度。
  • 空间复杂度：$O(1)$

优化的暴力法

思路

暴力法的时间复杂度为 $O(N ^ 3)$， 其中 $N$ 最大为 1000。一般来说， $O(N ^ 3)$ 的算法在数据量 <= 500 是可以 AC 的。1000 的数量级则需要考虑 $O(N ^ 2)$ 或者更好的解法。

OK，到这里了。我给大家一个干货。 应该是其他博主不太会提的。原因可能是他们不知道， 也可能是他们觉得太小儿科不需要说。

  1. 由于前面我根据数据规模推测到到了解法的复杂度区间是 $N ^ 2$, $N ^ 2 * logN$，不可能是 $N$ （WHY？）。
  2. 降低时间复杂度的方法主要有： 空间换时间 和 排序换时间（我们一般都是使用基于比较的排序方法）。而排序换时间仅仅在总体复杂度大于 $O(NlogN)$ 才适用（原因不用多说了吧？）。

这里由于总体的时间复杂度是 $O(N ^ 3)$，因此我自然想到了排序换时间。当我们对 nums 进行一次排序之后，我发现：

  • is_triangle 函数有一些判断是无效的
1
2
3
4
5
def is_triangle(self, a, b, c):
    if a == 0 or b == 0 or c == 0: return False
    # a + c > b 和  b + c > a 是无效的判断，因为恒成立
    if a + b > c and a + c > b and b + c > a: return True
    return False
  • 因此我们的目标变为找到a + b > c即可，因此第三层循环是可以提前退出的。
1
2
3
4
5
6
for i in range(n - 2):
    for j in range(i + 1, n - 1):
        k = j + 1
        while k < n and num[i] + nums[j] > nums[k]:
            k += 1
        ans += k - j - 1
  • 这也仅仅是减枝而已，复杂度没有变化。通过进一步观察，发现 k 没有必要每次都从 j + 1 开始。而是从上次找到的 k 值开始就行。原因很简单， 当 nums[i] + nums[j] > nums[k] 时，我们想要找到下一个满足 nums[i] + nums[j] > nums[k] 的 新的 k 值，由于进行了排序，因此这个 k 肯定比之前的大（单调递增性），因此上一个 k 值之前的数都是无效的，可以跳过。
1
2
3
4
5
6
for i in range(n - 2):
    k = i + 2
    for j in range(i + 1, n - 1):
        while k < n and nums[i] + nums[j] > nums[k]:
            k += 1
        ans += k - j - 1

由于 K 不会后退，因此最内层循环总共最多执行 N 次，因此总的时间复杂度为 $O(N ^ 2)$。

这个复杂度分析有点像单调栈，大家可以结合起来理解。

关键点分析

  • 排序

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def triangleNumber(self, nums: List[int]) -> int:
        n = len(nums)
        ans = 0
        nums.sort()
        for i in range(n - 2):
            if nums[i] == 0: continue
            k = i + 2
            for j in range(i + 1, n - 1):
                while k < n and nums[i] + nums[j] > nums[k]:
                    k += 1
                ans += k - j - 1
        return ans

复杂度分析

  • 时间复杂度：$O(N ^ 2)$
  • 空间复杂度：取决于排序算法

题目二

给你一个二叉树，实现固定值和的路径，优先层数低的，排在左边的

思路

DFS 找出所有的满足和为 target 的，遍历过程维护层数较低的并返回即可。 函数签名为：dfs(node, target, depth)，其中 node 为当前的节点， target 为目标和，减到 0 就找到目标路径了，depth 是深度，用于维护层数较低。

也可以使用 BFS 从左到右将 (node, target) 入队即可。

如果还不懂， 建议参考我的树专题

题目三

一组数据，找出能组成和被 6 整除的最大值对应的集合

题目描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
给你一个整数数组 nums，请你找出并返回能被六整除的元素最大和。


示例 1：

输入：nums = [3,6,5,1,8]
输出：18
解释：选出数字 3, 6, 1 和 8，它们的和是 18（可被 6 整除的最大和）。
示例 2：

输入：nums = [4]
输出：0
解释：4 不能被 6 整除，所以无法选出数字，返回 0。
示例 3：

输入：nums = [1,2,3,4,4]
输出：12
解释：选出数字 1, 3, 4 以及 4，它们的和是 12（可被 6 整除的最大和）。
 

提示：

1 <= nums.length <= 4 * 10^4
1 <= nums[i] <= 10^4

前置知识

  • 数组
  • 回溯法
  • 排序

公司

  • 字节
  • 网易有道

暴力法

思路

力扣类似题 1262. 可被三整除的最大和

这道题是 6 的倍数，而上面的是 3 的倍数。 实际上， 6 的倍数就是在满足三的倍数的条件下，再加上是偶数的条件即可。

这里以 3 的倍数为例，讲一下这道题。

一种方式是找出所有的能够被 3 整除的子集，然后挑选出和最大的。由于我们选出了所有的子集，那么时间复杂度就是 $O(2^N)$ ， 毫无疑问会超时。这里我们使用回溯法找子集，如果不清楚回溯法，可以参考我之前的题解，很多题目都用到了，比如78.subsets。

更多回溯题目，可以访问上方链接查看（可以使用一套模板搞定）：

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
    def maxSumDivThree(self, nums: List[int]) -> int:
        self.res = 0
        def backtrack(temp, start):
            total = sum(temp)
            if total % 3 == 0:
                self.res = max(self.res, total)
            for i in range(start, len(nums)):
                temp.append(nums[i])
                backtrack(temp, i + 1)
                temp.pop(-1)


        backtrack([], 0)

        return self.res

减法 + 排序

减法的核心思想是，我们求出总和。如果总和不满足题意，我们尝试减去最小的数，使之满足题意。

思路

这种算法的思想，具体来说就是：

  • 我们将所有的数字加起来，我们不妨设为 total
  • total 除以 3，得到一个余数 mod， mod 可能值有 0，1，2.
  • 同时我们建立两个数组，一个是余数为 1 的数组 one，一个是余数为 2 的数组 two
  • 如果 mod 为 0，我们直接返回即可。
  • 如果 mod 为 1，我们可以减去 one 数组中最小的一个（如果有的话），或者减去两个 two 数组中最小的（如果有的话），究竟减去谁取决谁更小。
  • 如果 mod 为 2，我们可以减去 two 数组中最小的一个（如果有的话），或者减去两个 one 数组中最小的（如果有的话），究竟减去谁取决谁更小。

由于我们需要取 one 和 two 中最小的一个或者两个，因此对数组 one 和 two 进行排序是可行的，如果基于排序的话，时间复杂度大致为 $O(NlogN)$，这种算法可以通过。

以题目中的例 1 为例：

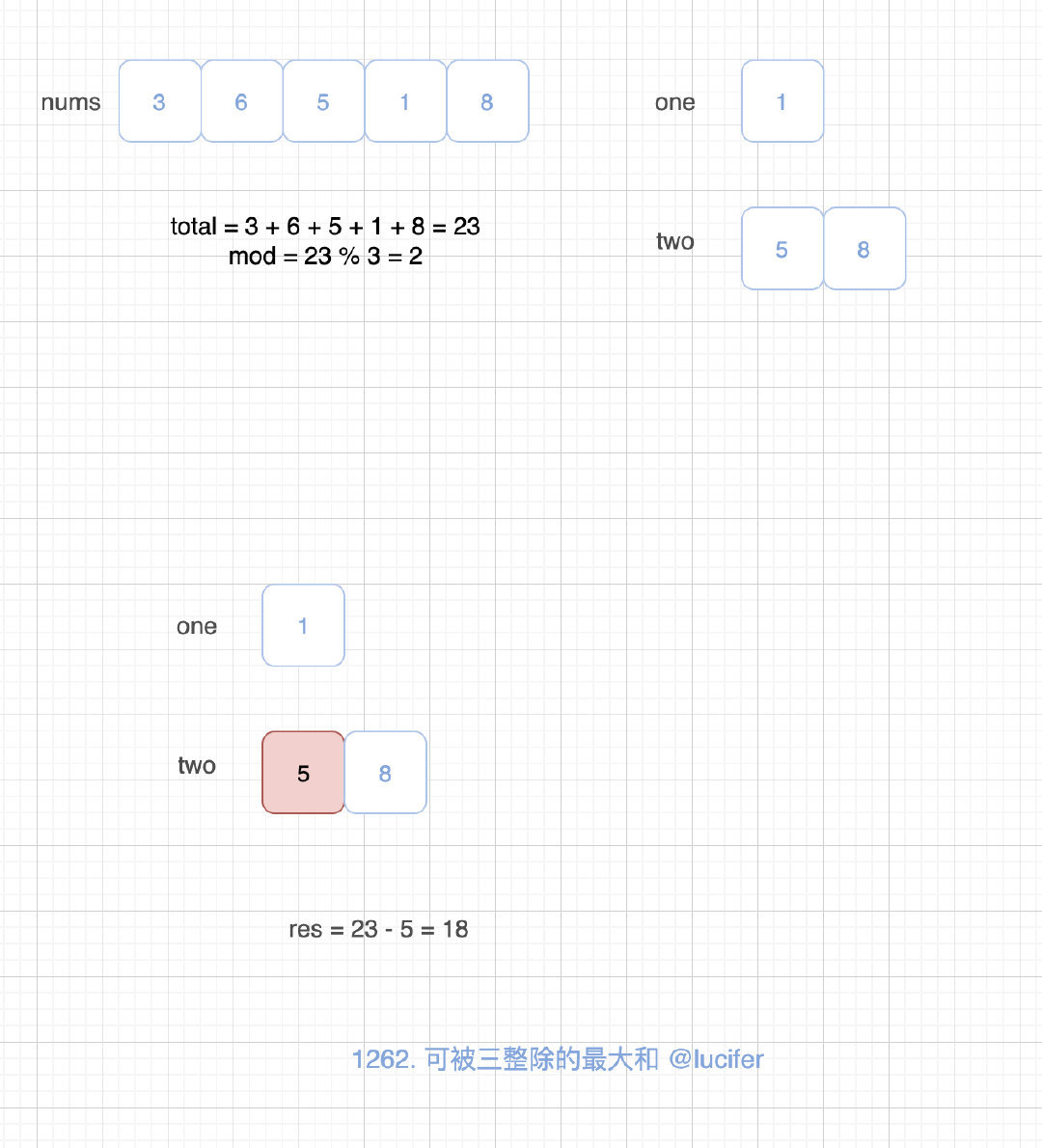
以题目中的例 2 为例：

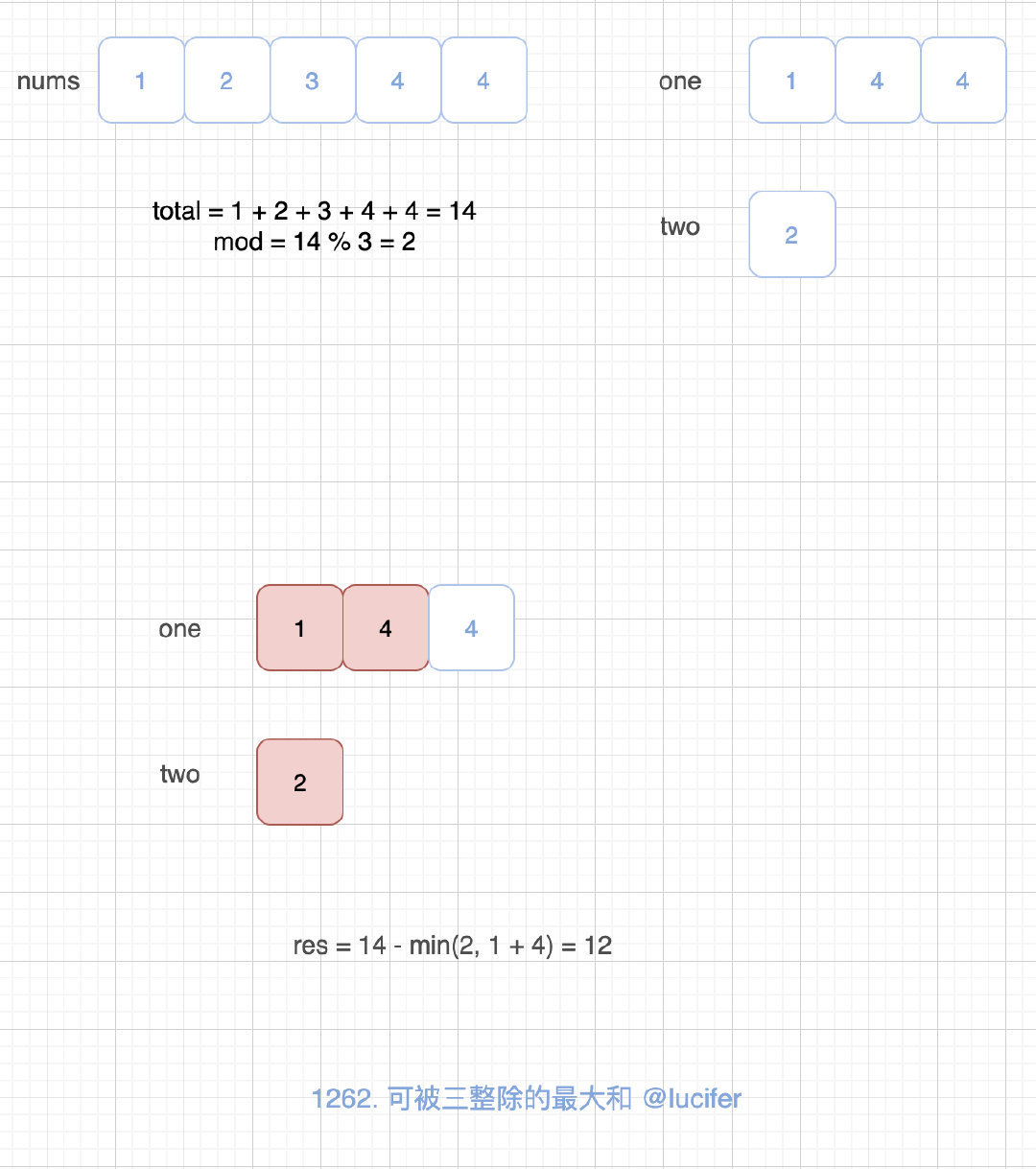
代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution:
    def maxSumDivThree(self, nums: List[int]) -> int:
        one = []
        two = []
        total = 0

        for num in nums:
            total += num
            if num % 3 == 1:
                one.append(num)
            if num % 3 == 2:
                two.append(num)
        one.sort()
        two.sort()
        if total % 3 == 0:
            return total
        elif total % 3 == 1 and one:
            if len(two) >= 2 and one[0] > two[0] + two[1]:
                return total - two[0] - two[1]
            return total - one[0]
        elif total % 3 == 2 and two:
            if len(one) >= 2 and two[0] > one[0] + one[1]:
                return total - one[0] - one[1]
            return total - two[0]
        return 0

减法 + 非排序

思路

上面的解法使用到了排序。 我们其实观察发现，我们只是用到了 one 和 two 的最小的两个数。因此我们完全可以在线形的时间和常数的空间完成这个算法。我们只需要分别记录 one 和 two 的最小值和次小值即可，在这里，我使用了两个长度为 2 的数组来表示，第一项是最小值，第二项是次小值。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution:
    def maxSumDivThree(self, nums: List[int]) -> int:
        one = [float('inf')] * 2
        two = [float('inf')] * 2
        total = 0

        for num in nums:
            total += num
            if num % 3 == 1:
                if num < one[0]:
                    t = one[0]
                    one[0] = num
                    one[1] = t
                elif num < one[1]:
                    one[1] = num
            if num % 3 == 2:
                if num < two[0]:
                    t = two[0]
                    two[0] = num
                    two[1] = t
                elif num < two[1]:
                    two[1] = num
        if total % 3 == 0:
            return total
        elif total % 3 == 1 and one:
            if len(two) >= 2 and one[0] > two[0] + two[1]:
                return total - two[0] - two[1]
            return total - one[0]
        elif total % 3 == 2 and two:
            if len(one) >= 2 and two[0] > one[0] + one[1]:
                return total - one[0] - one[1]
            return total - two[0]
        return 0

有限状态机

思路

我在数据结构与算法在前端领域的应用 - 第二篇 中讲到了有限状态机。

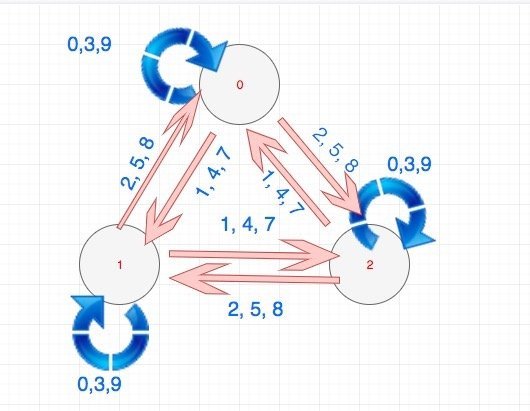
状态机表示若干个状态以及在这些状态之间的转移和动作等行为的数学模型。通俗的描述状态机就是定义了一套状态変更的流程：状态机包含一个状态集合，定义当状态机处于某一个状态的时候它所能接收的事件以及可执行的行为，执行完成后，状态机所处的状态。

状态机使用非常广泛，比如正则表达式的引擎，编译器的词法和语法分析，网络协议，企业应用等很多领域都会用到。

拿本题中来说，我们从左到右扫描数组的过程，将会不断改变状态机的状态。

我们使用 state 数组来表示本题的状态：

  • state[0] 表示 mod 为 0 的 最大和
  • state[1] 表示 mod 为 1 的 最大和
  • state[2] 表示 mod 为 1 的 最大和

我们的状态转移方程就会很容易。说到状态转移方程，你可能会想到动态规划。没错！这种思路可以直接翻译成动态规划，算法完全一样。如果你看过我上面提到的文章，那么状态转移方程对你来说就会很容易。如果你不清楚，那么请往下看：

  • 我们从左往右不断读取数字，我们不妨设这个数字为 num。
  • 如果 num % 3 为 0。 那么我们的 state[0], state[1], state[2] 可以直接加上 num（题目限定了 num 为非负）， 因为任何数字加上 3 的倍数之后，mod 3 的值是不变的。
  • 如果 num % 3 为 1。 我们知道 state[2] + num 会变成一个能被三整除的数，但是这个数字不一定比当前的 state[0]大。 代码表示就是max(state[2] + num, state[0])。同理 state[1] 和 state[2] 的转移逻辑类似。
  • 同理 num % 3 为 2 也是类似的逻辑。
  • 最后我们返回 state[0]即可。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    def maxSumDivThree(self, nums: List[int]) -> int:
        state = [0, float('-inf'), float('-inf')]

        for num in nums:
            if num % 3 == 0:
                state = [state[0] + num, state[1] + num, state[2] + num]
            if num % 3 == 1:
                a = max(state[2] + num, state[0])
                b = max(state[0] + num, state[1])
                c = max(state[1] + num, state[2])
                state = [a, b, c]
            if num % 3 == 2:
                a = max(state[1] + num, state[0])
                b = max(state[2] + num, state[1])
                c = max(state[0] + num, state[2])
                state = [a, b, c]
        return state[0]

当然这个代码还可以简化：

1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def maxSumDivThree(self, nums: List[int]) -> int:
        state = [0, float('-inf'), float('-inf')]

        for num in nums:
            temp = [0] * 3
            for i in range(3):
                temp[(i + num) % 3] = max(state[(i + num) % 3], state[i] + num)
            state = temp

        return state[0]

复杂度分析

  • 时间复杂度：$O(N)$
  • 空间复杂度：$O(1)$

关键点解析

  • 贪婪法
  • 状态机
  • 数学分析

扩展

实际上，我们可以采取加法（贪婪策略），感兴趣的可以试一下。

另外如果题目改成了请你找出并返回能被x整除的元素最大和，你只需要将我的解法中的 3 改成 x 即可。

题目四

题目描述

编辑距离变种，定义了编辑距离和两组字符串长度的比值，参考 https://leetcode-cn.com/problems/edit-distance/ ,只不过增删距离为 1，改距离为 2

思路

力扣原题变种 72. 编辑距离

这道题我太熟悉了，这道题用不同的语言我写了不下十次，提供了大概四五种写法（基本思路类似，写法不同）。然而笔试推荐大家记忆化递归来写，毕竟大多数笔试题解题速度比代码运行速度更重要。

代码

代码支持：Python3

Python3 Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution:
    @lru_cache(None)
    def helper(self, word1: str, s1: int, e1: int, word2: str, s2: int, e2: int) -> int:
        if s1 > e1:
            return e2 - s2 + 1
        elif s2 > e2:
            return e1 - s1 + 1
        c1 = word1[s1]
        c2 = word2[s2]
        if c1 == c2:
            return self.helper(word1, s1 + 1, e1, word2, s2 + 1, e2)
        else:
            return  (
                min(
                    self.helper(word1, s1 + 1, e1, word2, s2, e2) + 1,  # delete or add
                    self.helper(word1, s1, e1, word2, s2 + 1, e2) + 1,  # delete or add
                    self.helper(word1, s1 + 1, e1, word2, s2 + 1, e2) + 2,  # replace
                )
            )

    def minDistance(self, word1: str, word2: str) -> int:
        return self.helper(word1, 0, len(word1) - 1, word2, 0, len(word2) - 1)

复杂度分析

令 m 和 n 分别为两个字符串的长度。

  • 时间复杂度：$O(m * n)$
  • 空间复杂度：$O(max(m, n))$

 上一页

前端 面经 校招 虾皮

 评论


博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本站使用 Material X 作为主题 。
载入天数...载入时分秒...