几乎刷完了力扣所有的堆题，我发现了这些东西。。。（第二弹）

一点题外话

上次在我的公众号给大家做了一个小调查《投出你想要的题解编程语言吧~》。以下是调查的结果：

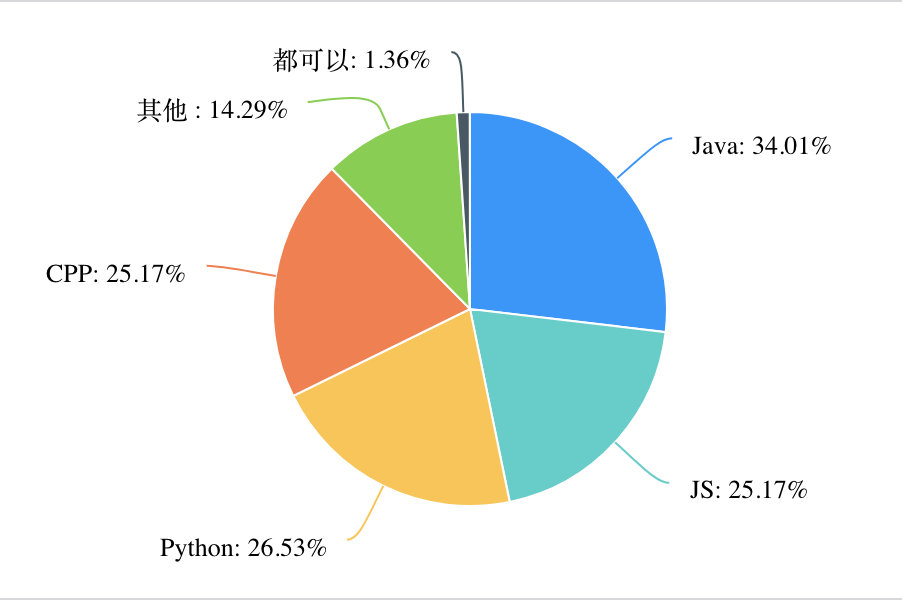
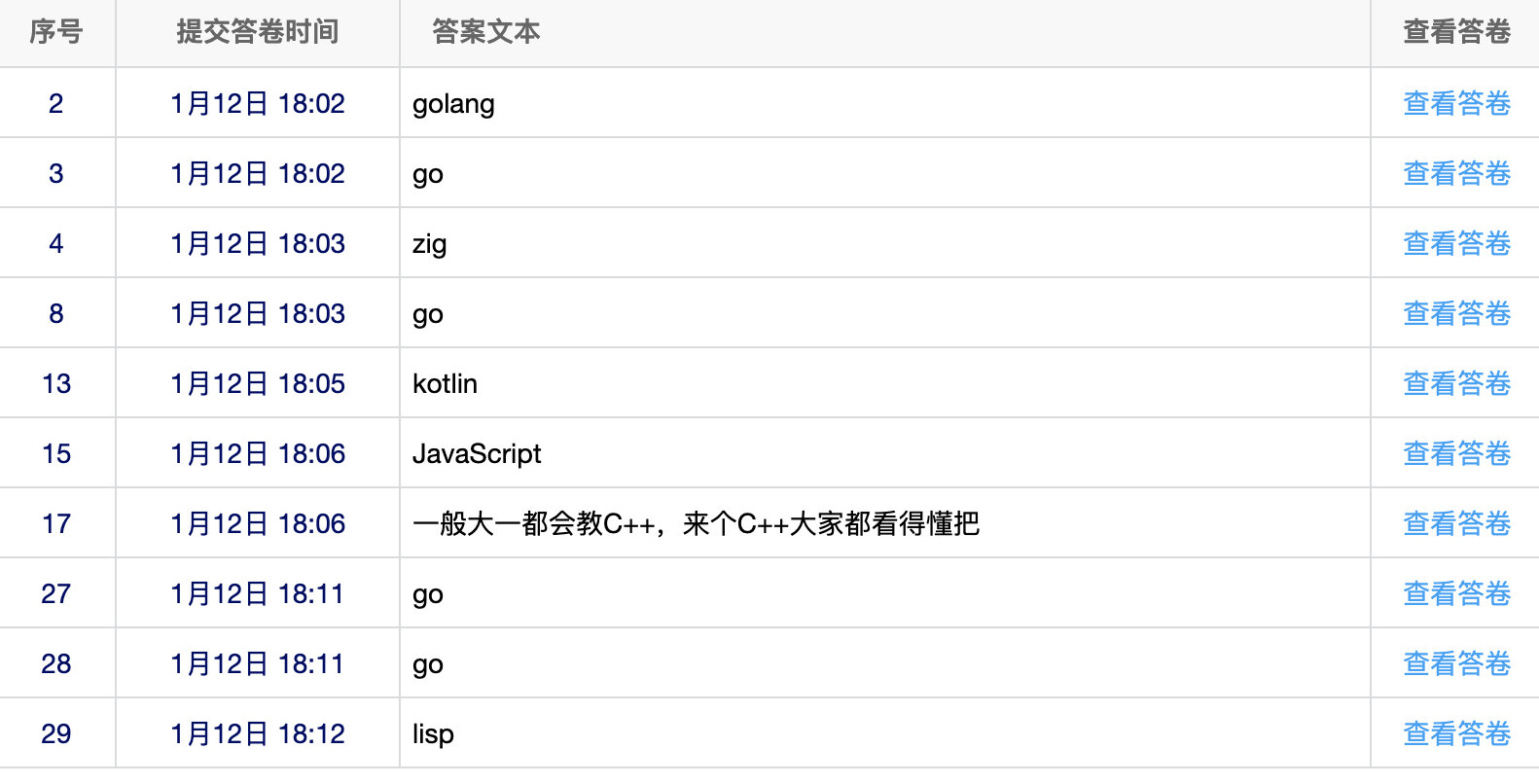
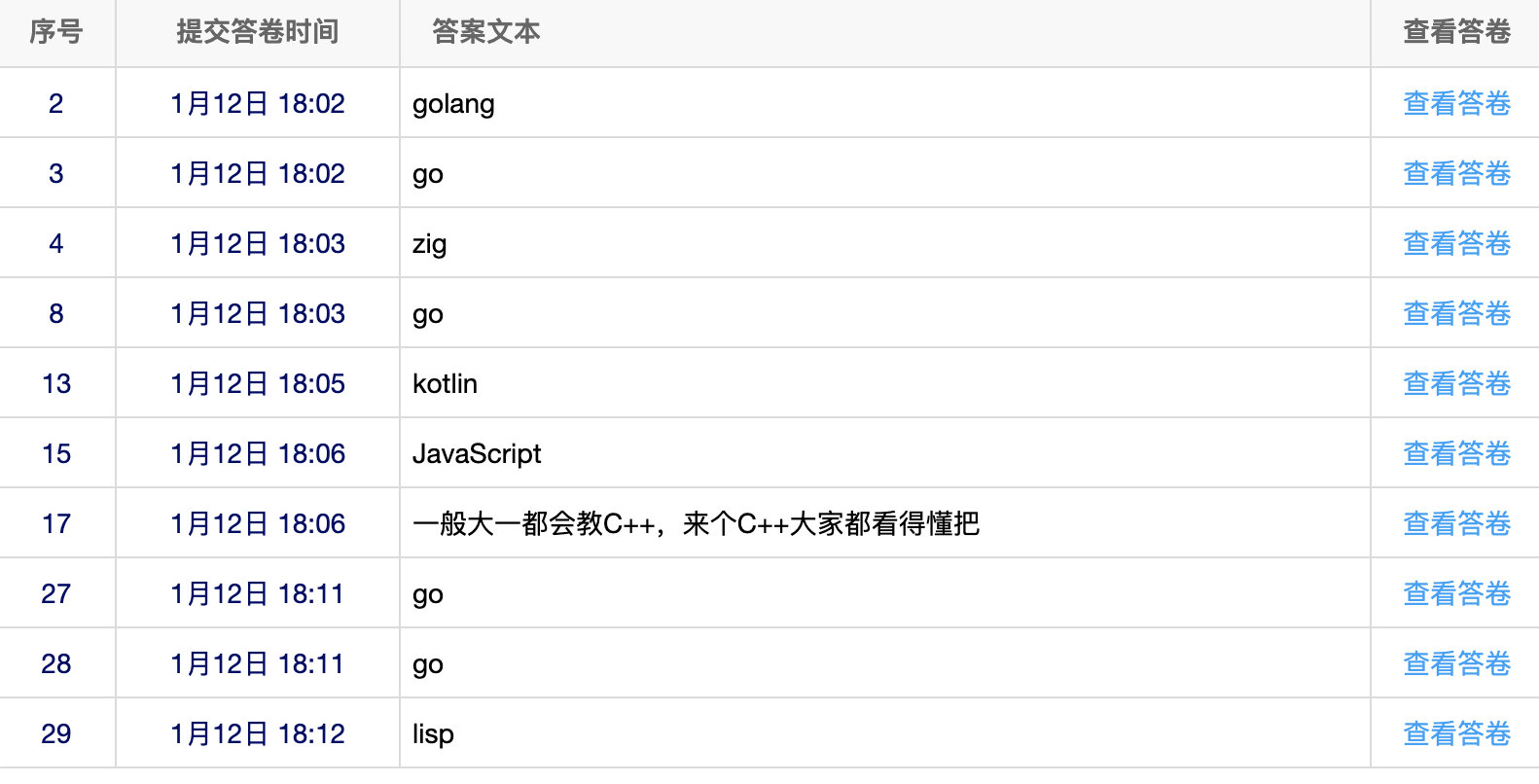
而关于其他，则大多数是 Go 语言。

由于 Java 和 Python 所占比例已经超过了 60%，这次我尝试一下 Java 和 Python 双语言来写，感谢 @CaptainZ 提供的 Java 代码。同时为了不让文章又臭又长，我将 Java 本文所有代码（Java 和 Python）都放到了力扣加加官网上，网站地址：https://leetcode-solution.cn/solution-code

如果不科学上网的话，可能打开会很慢。

正文

大家好，我是 lucifer。今天给大家带来的是《堆》专题。先上下本文的提纲，这个是我用 mindmap 画的一个脑图，之后我会继续完善，将其他专题逐步完善起来。

大家也可以使用 vscode blink-mind 打开源文件查看，里面有一些笔记可以点开查看。源文件可以去我的公众号《力扣加加》回复脑图获取，以后脑图也会持续更新更多内容。vscode 插件地址：https://marketplace.visualstudio.com/items?itemName=awehook.vscode-blink-mind

本系列包含以下专题：

• 几乎刷完了力扣所有的链表题，我发现了这些东西。。。
• 几乎刷完了力扣所有的树题，我发现了这些东西。。。
• 几乎刷完了力扣所有的堆题，我发现了这些东西。。。（第一弹）

本次是下篇，没有看过上篇的同学强烈建议先阅读上篇几乎刷完了力扣所有的堆题，我发现了这些东西。。。(第一弹)

这是第二部分，后面的内容更加干货，分别是三个技巧和四大应用。这两个主题是专门教你怎么解题的。掌握了它，力扣中的大多数堆的题目都不在话下（当然我指的仅仅是题目中涉及到堆的部分）。

警告： 本章的题目基本都是力扣 hard 难度，这是因为堆的题目很多标记难度都不小，关于这点在前面也介绍过了。

一点说明

在上主菜之前，先给大家来个开胃菜。

这里给大家介绍两个概念，分别是元组和模拟大顶堆 。之所以进行这些说明就是防止大家后面看不懂。

元组

使用堆不仅仅可以存储单一值，比如 [1,2,3,4] 的 1，2，3，4 分别都是单一值。除了单一值，也可以存储复合值，比如对象或者元组等。

这里我们介绍一种存储元组的方式，这个技巧会在后面被广泛使用，请务必掌握。比如 [(1,2,3), (4,5,6), (2,1,3),(4,2,8)]。

h = [(1,2,3), (4,5,6), (2,1,3),(4,2,8)]
heapq.heappify(h) # 堆化（小顶堆）

heapq.heappop() # 弹出 (1,2,3)
heapq.heappop() # 弹出 (2,1,3)
heapq.heappop() # 弹出 (4,2,8)
heapq.heappop() # 弹出 (4,5,6)

用图来表示堆结构就是下面这样：

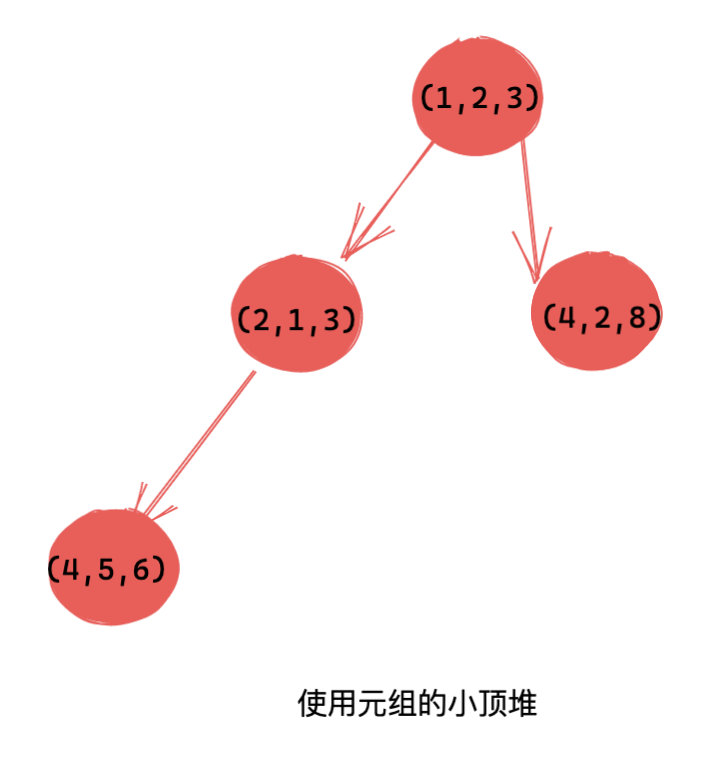
简单解释一下上面代码的执行结果。

使用元组的方式，默认将元组第一个值当做键来比较。如果第一个相同，继续比较第二个。比如上面的 (4,5,6) 和 (4,2,8)，由于第一个值相同，因此继续比较后一个，又由于 5 比 2 大，因此 (4,2,8)先出堆。

使用这个技巧有两个作用：

1. 携带一些额外的信息。 比如我想求二维矩阵中第 k 小数，当然是以值作为键。但是处理过程又需要用到其行和列信息，那么使用元组就很合适，比如 (val, row, col)这样的形式。

2. 想根据两个键进行排序，一个主键一个副键。这里面又有两种典型的用法，

   2.1 一种是两个都是同样的顺序，比如都是顺序或者都是逆序。

   2.2 另一种是两个不同顺序排序，即一个是逆序一个是顺序。

由于篇幅原因，具体就不再这里展开了，大家在平时做题过程中留意可以一下，有机会我会单独开一篇文章讲解。

如果你所使用的编程语言没有堆或者堆的实现不支持元组，那么也可以通过简单的改造使其支持，主要就是自定义比较逻辑即可。

模拟大顶堆

由于 Python 没有大顶堆。因此我这里使用了小顶堆进行模拟实现。即将原有的数全部取相反数，比如原数字是 5，就将 -5 入堆。经过这样的处理，小顶堆就可以当成大顶堆用了。不过需要注意的是，当你 pop 出来的时候， 记得也要取反，将其还原回来哦。

代码示例：

h = []
A = [1,2,3,4,5]
for a in A:
    heapq.heappush(h, -a)
-1 * heapq.heappop(h) # 5
-1 * heapq.heappop(h) # 4
-1 * heapq.heappop(h) # 3
-1 * heapq.heappop(h) # 2
-1 * heapq.heappop(h) # 1

用图来表示就是下面这样：

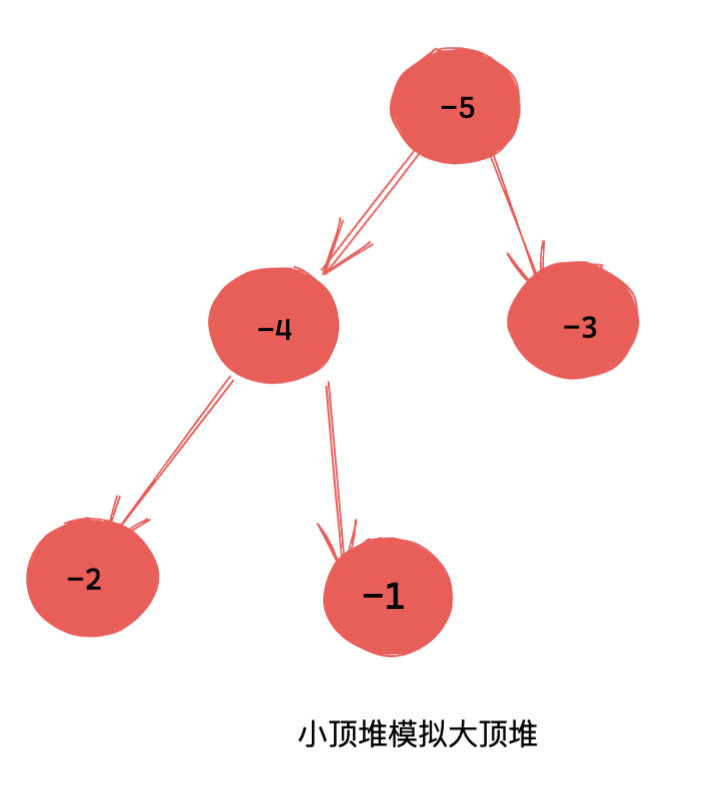
铺垫就到这里，接下来进入正题。

三个技巧

技巧一 - 固定堆

这个技巧指的是固定堆的大小 k 不变，代码上可通过每 pop 出去一个就 push 进来一个来实现。而由于初始堆可能是 0，我们刚开始需要一个一个 push 进堆以达到堆的大小为 k，因此严格来说应该是维持堆的大小不大于 k。

固定堆一个典型的应用就是求第 k 小的数。其实求第 k 小的数最简单的思路是建立小顶堆，将所有的数先全部入堆，然后逐个出堆，一共出堆 k 次。最后一次出堆的就是第 k 小的数。

然而，我们也可不先全部入堆，而是建立大顶堆（注意不是上面的小顶堆），并维持堆的大小为 k 个。如果新的数入堆之后堆的大小大于 k，则需要将堆顶的数和新的数进行比较，并将较大的移除。这样可以保证堆中的数是全体数字中最小的 k 个，而这最小的 k 个中最大的（即堆顶）不就是第 k 小的么？这也就是选择建立大顶堆，而不是小顶堆的原因。

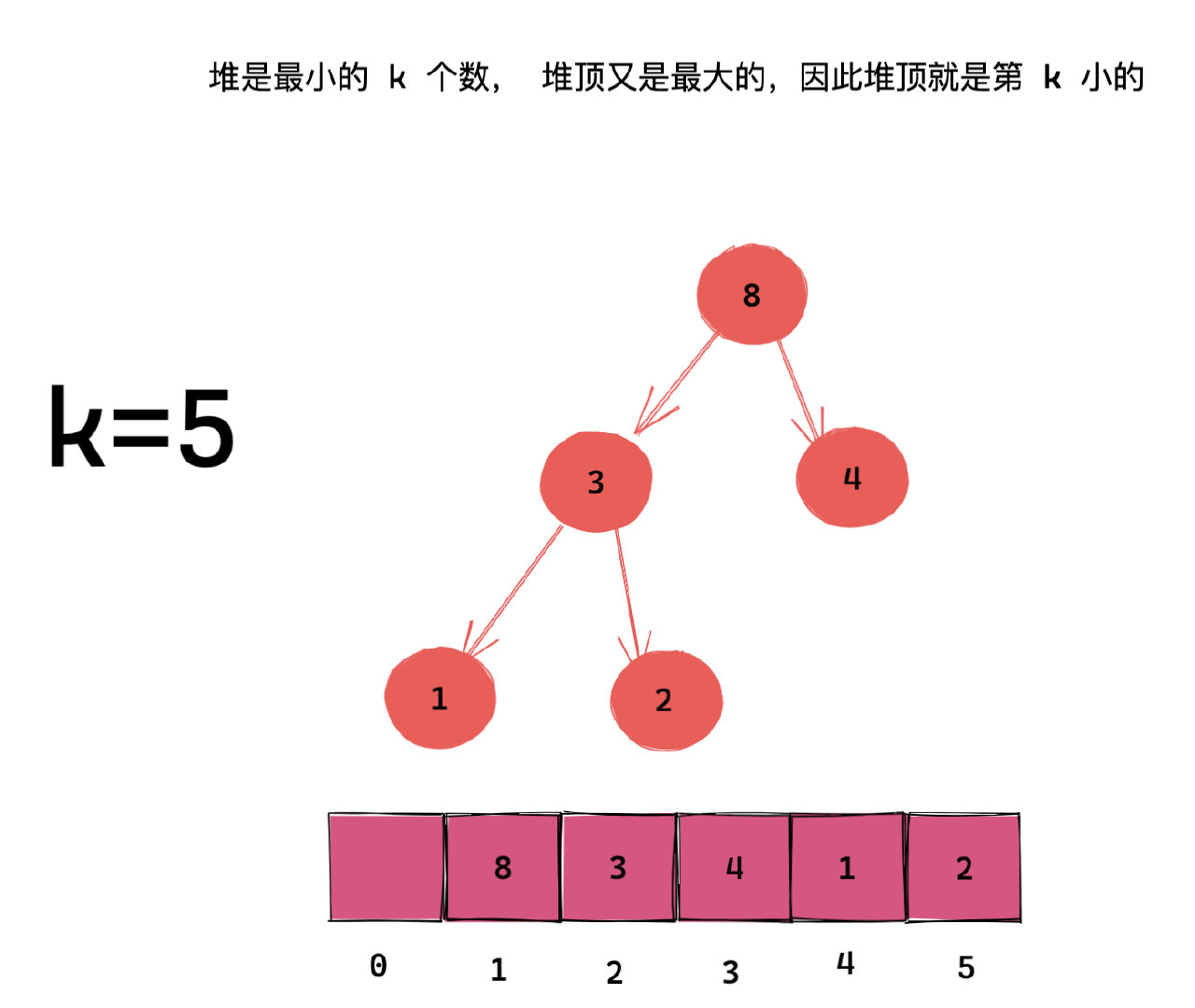
简单一句话总结就是固定一个大小为 k 的大顶堆可以快速求第 k 小的数，反之固定一个大小为 k 的小顶堆可以快速求第 k 大的数。比如力扣 2020-02-24 的周赛第三题5663. 找出第 K 大的异或坐标值就可以用固定小顶堆技巧来实现（这道题让你求第 k 大的数）。

这么说可能你的感受并不强烈，接下来我给大家举两个例子来帮助大家加深印象。

295. 数据流的中位数

题目描述

中位数是有序列表中间的数。如果列表长度是偶数，中位数则是中间两个数的平均值。

例如，

[2,3,4]  的中位数是 3

[2,3] 的中位数是 (2 + 3) / 2 = 2.5

设计一个支持以下两种操作的数据结构：

void addNum(int num) - 从数据流中添加一个整数到数据结构中。
double findMedian() - 返回目前所有元素的中位数。
示例：

addNum(1)
addNum(2)
findMedian() -> 1.5
addNum(3)
findMedian() -> 2
进阶:

如果数据流中所有整数都在 0 到 100 范围内，你将如何优化你的算法？
如果数据流中 99% 的整数都在 0 到 100 范围内，你将如何优化你的算法？

思路

这道题实际上可看出是求第 k 小的数的特例了。

• 如果列表长度是奇数，那么 k 就是 (n + 1) / 2，中位数就是第 k 个数，。比如 n 是 5， k 就是 (5 + 1)/ 2 = 3。
• 如果列表长度是偶数，那么 k 就是 (n + 1) / 2 和 (n + 1) / 2 + 1，中位数则是这两个数的平均值。比如 n 是 6， k 就是 (6 + 1)/ 2 = 3 和 (6 + 1) / 2 + 1 = 4。

因此我们的可以维护两个固定堆，固定堆的大小为 $(n + 1) \div 2$ 和 $n - (n + 1)\div2$，也就是两个堆的大小最多相差 1，更具体的就是 $ 0 <= (n + 1) \div 2 - (n - (n + 1) \div 2) <= 1$。

基于上面提到的知识，我们可以：

• 建立一个大顶堆，并存放最小的 $(n + 1) \div 2$ 个数，这样堆顶的数就是第 $(n + 1) \div 2$ 小的数，也就是奇数情况的中位数。
• 建立一个小顶堆，并存放最大的 n - $(n + 1) \div 2$ 个数，这样堆顶的数就是第 n - $(n + 1) \div 2$ 大的数，结合上面的大顶堆，可求出偶数情况的中位数。

有了这样一个知识，剩下的只是如何维护两个堆的大小了。

• 如果大顶堆的个数比小顶堆少，那么就将小顶堆中最小的转移到大顶堆。而由于小顶堆维护的是最大的 k 个数，大顶堆维护的是最小的 k 个数，因此小顶堆堆顶一定大于等于大顶堆堆顶，并且这两个堆顶是此时的中位数。
• 如果大顶堆的个数比小顶堆的个数多 2，那么就将大顶堆中最大的转移到小顶堆，理由同上。

至此，可能你已经明白了为什么分别建立两个堆，并且需要一个大顶堆一个小顶堆。这其中的原因正如上面所描述的那样。

固定堆的应用常见还不止于此，我们继续看一道题。

代码

class MedianFinder:
    def __init__(self):
        self.min_heap = []
        self.max_heap = []
    def addNum(self, num: int) -> None:
        if not self.max_heap or num < -self.max_heap[0]:
            heapq.heappush(self.max_heap, -num)
        else:
            heapq.heappush(self.min_heap, num)
        if len(self.max_heap) > len(self.min_heap) + 1:
            heappush(self.min_heap, -heappop(self.max_heap))
        elif len(self.min_heap) > len(self.max_heap):
            heappush(self.max_heap, -heappop(self.min_heap))
    def findMedian(self) -> float:
        if len(self.min_heap) == len(self.max_heap): return (self.min_heap[0] - self.max_heap[0]) / 2
        return -self.max_heap[0]

(代码 1.3.1)

857. 雇佣 K 名工人的最低成本

题目描述

有 N 名工人。 第 i 名工人的工作质量为 quality[i] ，其最低期望工资为 wage[i] 。

现在我们想雇佣 K 名工人组成一个工资组。在雇佣 一组 K 名工人时，我们必须按照下述规则向他们支付工资：

对工资组中的每名工人，应当按其工作质量与同组其他工人的工作质量的比例来支付工资。
工资组中的每名工人至少应当得到他们的最低期望工资。
返回组成一个满足上述条件的工资组至少需要多少钱。

 

示例 1：

输入： quality = [10,20,5], wage = [70,50,30], K = 2
输出： 105.00000
解释： 我们向 0 号工人支付 70，向 2 号工人支付 35。
示例 2：

输入： quality = [3,1,10,10,1], wage = [4,8,2,2,7], K = 3
输出： 30.66667
解释： 我们向 0 号工人支付 4，向 2 号和 3 号分别支付 13.33333。
 

提示：

1 <= K <= N <= 10000，其中 N = quality.length = wage.length
1 <= quality[i] <= 10000
1 <= wage[i] <= 10000
与正确答案误差在 10^-5 之内的答案将被视为正确的。

思路

题目要求我们选择 k 个人，按其工作质量与同组其他工人的工作质量的比例来支付工资，并且工资组中的每名工人至少应当得到他们的最低期望工资。

换句话说，同一组的 k 个人他们的工作质量和工资比是一个固定值才能使支付的工资最少。请先理解这句话，后面的内容都是基于这个前提产生的。

我们不妨定一个指标工作效率，其值等于 q / w。前面说了这 k 个人的 q / w 是相同的才能保证工资最少，并且这个 q / w 一定是这 k 个人最低的（短板），否则一定会有人得不到最低期望工资。

于是我们可以写出下面的代码：

class Solution:
    def mincostToHireWorkers(self, quality: List[int], wage: List[int], K: int) -> float:
        eff = [(q / w, q, w) for a, b in zip(quality, wage)]
        eff.sort(key=lambda a: -a[0])
        ans = float('inf')
        for i in range(K-1, len(eff)):
            h = []
            k = K - 1
            rate, _, total = eff[i]
            # 找出工作效率比它高的 k 个人，这 k 个人的工资尽可能低。
            # 由于已经工作效率倒序排了，因此前面的都是比它高的，然后使用堆就可得到 k 个工资最低的。
            for j in range(i):
                heapq.heappush(h, eff[j][1] / rate)
            while k > 0:
                total += heapq.heappop(h)
                k -= 1
            ans = min(ans, total)
        return ans

(代码 1.3.2)

这种做法每次都 push 很多数，并 pop k 次，并没有很好地利用堆的动态特性，而只利用了其求极值的特性。

一个更好的做法是使用固定堆技巧。

这道题可以换个角度思考。其实这道题不就是让我们选 k 个人，工作效率比取他们中最低的，并按照这个最低的工作效率计算总工资，找出最低的总工资么？ 因此这道题可以固定一个大小为 k 的大顶堆，通过一定操作保证堆顶的就是第 k 小的（操作和前面的题类似）。

并且前面的解法中堆使用了三元组 (q / w, q, w)，实际上这也没有必要。因为已知其中两个，可推导出另外一个，因此存储两个就行了，而又由于我们需要根据工作效率比做堆的键，因此任意选一个 q 或者 w 即可，这里我选择了 q，即存 (q/2, q) 二元组。

具体来说就是：以 rate 为最低工作效率比的 k 个人的总工资 = $\displaystyle \sum_{n=1}^{k}{q}_{n}/rate$，这里的 rate 就是当前的 q / w，同时也是 k 个人的 q / w 的最小值。

代码

class Solution:
    def mincostToHireWorkers(self, quality: List[int], wage: List[int], K: int) -> float:
        effs = [(q / w, q) for q, w in zip(quality, wage)]
        effs.sort(key=lambda a: -a[0])
        ans = float('inf')
        h = []
        total = 0
        for rate, q in effs:
            heapq.heappush(h, -q)
            total += q
            if len(h) > K:
                total += heapq.heappop(h)
            if len(h) == K:
                ans = min(ans, total / rate)
        return ans

(代码 1.3.3)

技巧二 - 多路归并

这个技巧其实在前面讲超级丑数的时候已经提到了，只是没有给这种类型的题目一个名字。

其实这个技巧，叫做多指针优化可能会更合适，只不过这个名字实在太过朴素且容易和双指针什么的混淆，因此我给 ta 起了个别致的名字 - 多路归并。

• 多路体现在：有多条候选路线。代码上，我们可使用多指针来表示。
• 归并体现在：结果可能是多个候选路线中最长的或者最短，也可能是第 k 个 等。因此我们需要对多条路线的结果进行比较，并根据题目描述舍弃或者选取某一个或多个路线。

这样描述比较抽象，接下来通过几个例子来加深一下大家的理解。

这里我给大家精心准备了四道难度为 hard 的题目。 掌握了这个套路就可以去快乐地 AC 这四道题啦。

1439. 有序矩阵中的第 k 个最小数组和

题目描述

给你一个 m * n 的矩阵 mat，以及一个整数 k ，矩阵中的每一行都以非递减的顺序排列。

你可以从每一行中选出 1 个元素形成一个数组。返回所有可能数组中的第 k 个 最小 数组和。

 

示例 1：

输入：mat = [[1,3,11],[2,4,6]], k = 5
输出：7
解释：从每一行中选出一个元素，前 k 个和最小的数组分别是：
[1,2], [1,4], [3,2], [3,4], [1,6]。其中第 5 个的和是 7 。
示例 2：

输入：mat = [[1,3,11],[2,4,6]], k = 9
输出：17
示例 3：

输入：mat = [[1,10,10],[1,4,5],[2,3,6]], k = 7
输出：9
解释：从每一行中选出一个元素，前 k 个和最小的数组分别是：
[1,1,2], [1,1,3], [1,4,2], [1,4,3], [1,1,6], [1,5,2], [1,5,3]。其中第 7 个的和是 9 。
示例 4：

输入：mat = [[1,1,10],[2,2,9]], k = 7
输出：12
 

提示：

m == mat.length
n == mat.length[i]
1 <= m, n <= 40
1 <= k <= min(200, n ^ m)
1 <= mat[i][j] <= 5000
mat[i] 是一个非递减数组

思路

其实这道题就是给你 m 个长度均相同的一维数组，让我们从这 m 个数组中分别选出一个数，即一共选取 m 个数，求这 m 个数的和是所有选取可能性中和第 k 小的。

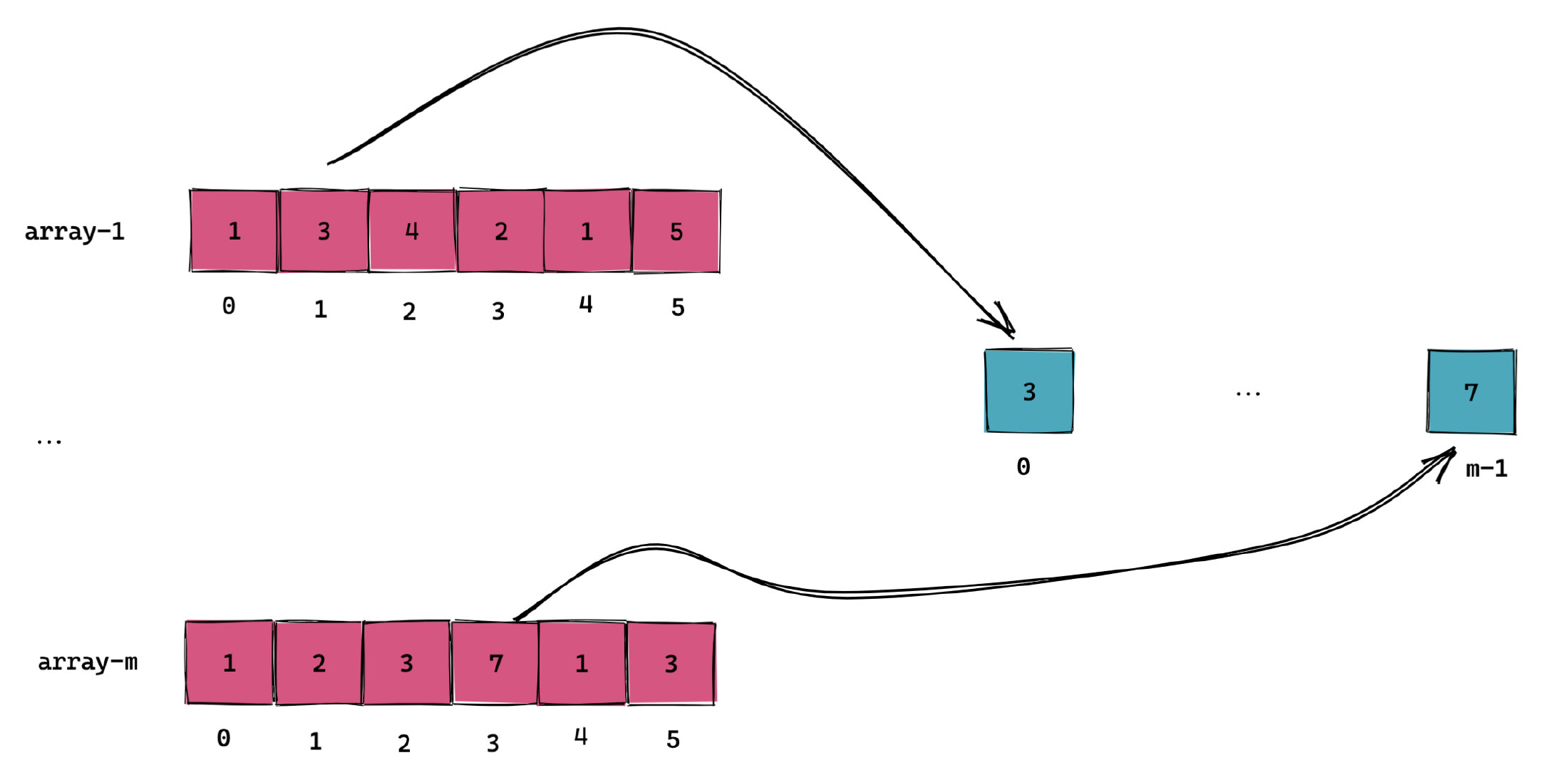
一个朴素的想法是使用多指针来解。对于这道题来说就是使用 m 个指针，分别指向 m 个一维数组，指针的位置表示当前选取的是该一维数组中第几个。

以题目中的 mat = [[1,3,11],[2,4,6]], k = 5 为例。

• 先初始化两个指针 p1,p2，分别指向两个一维数组的开头，代码表示就是全部初始化为 0。
• 此时两个指针指向的数字和为 1 + 2 = 3，这就是第 1 小的和。
• 接下来，我们移动其中一个指针。此时我们可以移动 p1，也可以移动 p2。
• 那么第 2 小的一定是移动 p1 和 移动 p2 这两种情况的较小值。而这里移动 p1 和 p2 实际上都会得到 5，也就是说第 2 和第 3 小的和都是 5。

到这里已经分叉了，出现了两种情况(注意看粗体的位置，粗体表示的是指针的位置)：

1. [1,3,11],[2,4,6] 和为 5
2. [1,3,11],[2,4,6] 和为 5

接下来，这两种情况应该齐头并进，共同进行下去。

对于情况 1 来说，接下来移动又有两种情况。

1. [1,3,11],[2,4,6] 和为 13
2. [1,3,11],[2,4,6] 和为 7

对于情况 2 来说，接下来移动也有两种情况。

1. [1,3,11],[2,4,6] 和为 7
2. [1,3,11],[2,4,6] 和为 7

我们通过比较这四种情况，得出结论： 第 4，5，6 小的数都是 7。但第 7 小的数并不一定是 13。原因和上面类似，可能第 7 小的就隐藏在前面的 7 分裂之后的新情况中，实际上确实如此。因此我们需要继续执行上述逻辑。

进一步，我们可以将上面的思路拓展到一般情况。

上面提到了题目需要求的其实是第 k 小的和，而最小的我们是容易知道的，即所有的一维数组首项和。我们又发现，根据最小的，我们可以推导出第 2 小，推导的方式就是移动其中一个指针，这就一共分裂出了 n 种情况了，其中 n 为一维数组长度，第 2 小的就在这分裂中的 n 种情况中，而筛选的方式是这 n 种情况和最小的，后面的情况也是类似。不难看出每次分裂之后极值也发生了变化，因此这是一个明显的求动态求极值的信号，使用堆是一个不错的选择。

那代码该如何书写呢？

上面说了，我们先要初始化 m 个指针，并赋值为 0。对应伪代码：

# 初始化堆
h = []
# sum(vec[0] for vec in mat) 是 m 个一维数组的首项和
# [0] * m 就是初始化了一个长度为 m 且全部填充为 0 的数组。
# 我们将上面的两个信息组装成元祖 cur 方便使用
cur = (sum(vec[0] for vec in mat), [0] * m)
# 将其入堆
heapq.heappush(h, cur)

接下来，我们每次都移动一个指针，从而形成分叉出一条新的分支。每次从堆中弹出一个最小的，弹出 k 次就是第 k 小的了。伪代码：

for 1 to K:
    # acc 当前的和， pointers 是指针情况。
    acc, pointers = heapq.heappop(h)
    # 每次都粗暴地移动指针数组中的一个指针。每移动一个指针就分叉一次， 一共可能移动的情况是 n，其中 n 为一维数组的长度。
    for i, pointer in enumerate(pointers):
        # 如果 pointer == len(mat[0]) - 1 说明到头了，不能移动了
        if pointer != len(mat[0]) - 1:
            # 下面两句话的含义是修改 pointers[i] 的指针 为 pointers[i] + 1
            new_pointers = pointers.copy()
            new_pointers[i] += 1
            # 将更新后的 acc 和指针数组重新入堆
            heapq.heappush(h, (acc + mat[i][pointer + 1] - mat[i][pointer], new_pointers))

这是多路归并问题的核心代码，请务必记住。

代码看起来很多，其实去掉注释一共才七行而已。

上面的伪代码有一个问题。比如有两个一维数组，指针都初始化为 0。第一次移动第一个一维数组的指针，第二次移动第二个数组的指针，此时指针数组为 [1, 1]，即全部指针均指向下标为 1 的元素。而如果第一次移动第二个一维数组的指针，第二次移动第一个数组的指针，此时指针数组仍然为 [1, 1]。这实际上是一种情况，如果不加控制会被计算两次导致出错。

一个可能的解决方案是使用 hashset 记录所有的指针情况，这样就避免了同样的指针被计算多次的问题。为了做到这一点，我们需要对指针数组的使用做一些微调，即使用元组代替数组。原因在于数组是无法直接哈希化的。具体内容请参考代码区。

多路归并的题目，思路和代码都比较类似。为了后面的题目能够更高地理解，请务必搞定这道题，后面我们将不会这么详细地进行分析。

代码

class Solution:
    def kthSmallest(self, mat, k: int) -> int:
        h = []
        cur = (sum(vec[0] for vec in mat), tuple([0] * len(mat)))
        heapq.heappush(h, cur)
        seen = set(cur)

        for _ in range(k):
            acc, pointers = heapq.heappop(h)
            for i, pointer in enumerate(pointers):
                if pointer != len(mat[0]) - 1:
                    t = list(pointers)
                    t[i] = pointer + 1
                    tt = tuple(t)
                    if tt not in seen:
                        seen.add(tt)
                        heapq.heappush(h, (acc + mat[i][pointer + 1] - mat[i][pointer], tt))
        return acc

(代码 1.3.4)

719. 找出第 k 小的距离对

题目描述

给定一个整数数组，返回所有数对之间的第 k 个最小距离。一对 (A, B) 的距离被定义为 A 和 B 之间的绝对差值。

示例 1:

输入：
nums = [1,3,1]
k = 1
输出：0
解释：
所有数对如下：
(1,3) -> 2
(1,1) -> 0
(3,1) -> 2
因此第 1 个最小距离的数对是 (1,1)，它们之间的距离为 0。
提示:

2 <= len(nums) <= 10000.
0 <= nums[i] < 1000000.
1 <= k <= len(nums) * (len(nums) - 1) / 2.

思路

不难看出所有的数对可能共 $C_n^2$ 个，也就是 $n\times(n-1)\div2$。

因此我们可以使用两次循环找出所有的数对，并升序排序，之后取第 k 个。

实际上，我们可使用固定堆技巧，维护一个大小为 k 的大顶堆，这样堆顶的元素就是第 k 小的，这在前面的固定堆中已经讲过，不再赘述。

class Solution:
    def smallestDistancePair(self, nums: List[int], k: int) -> int:
        h = []
        for i in range(len(nums)):
            for j in range(i + 1, len(nums)):
                a, b = nums[i], nums[j]
                # 维持堆大小不超过 k
                if len(h) == k and -abs(a - b) > h[0]:
                    heapq.heappop(h)
                if len(h) < k:
                    heapq.heappush(h, -abs(a - b))

        return -h[0]

(代码 1.3.5)

不过这种优化意义不大，因为算法的瓶颈在于 $N^2$ 部分的枚举，我们应当设法优化这一点。

如果我们将数对进行排序，那么最小的数对距离一定在 nums[i] - nums[i - 1] 中，其中 i 为从 1 到 n 的整数，究竟是哪个取决于谁更小。接下来就可以使用上面多路归并的思路来解决了。

如果 nums[i] - nums[i - 1] 的差是最小的，那么第 2 小的一定是剩下的 n - 1 种情况和 nums[i] - nums[i - 1] 分裂的新情况。关于如何分裂，和上面类似，我们只需要移动其中 i 的指针为 i + 1 即可。这里的指针数组长度固定为 2，而不是上面题目中的 m。这里我将两个指针分别命名为 fr 和 to，分别代表 from 和 to。

代码

class Solution(object):
    def smallestDistancePair(self, nums, k):
        nums.sort()
        # n 种候选答案
        h = [(nums[i+1] - nums[i], i, i+1) for i in range(len(nums) - 1)]
        heapq.heapify(h)

        for _ in range(k):
            diff, fr, to = heapq.heappop(h)
            if to + 1 < len(nums):
                heapq.heappush((nums[to + 1] - nums[fr], fr, to + 1))

        return diff

(代码 1.3.6)

由于时间复杂度和 k 有关，而 k 最多可能达到 $N^2$ 的量级，因此此方法实际上也会超时。不过这证明了这种思路的正确性，如果题目稍加改变说不定就能用上。

这道题可通过二分法来解决，由于和堆主题有偏差，因此这里简单讲一下。

求第 k 小的数比较容易想到的就是堆和二分法。二分的原因在于求第 k 小，本质就是求不大于其本身的有 k - 1 个的那个数。而这个问题很多时候满足单调性，因此就可使用二分来解决。

以这道题来说，最大的数对差就是数组的最大值 - 最小值，不妨记为 max_diff。我们可以这样发问：

• 数对差小于 max_diff 的有几个？
• 数对差小于 max_diff - 1 的有几个？
• 数对差小于 max_diff - 2 的有几个？
• 数对差小于 max_diff - 3 的有几个？
• 数对差小于 max_diff - 4 的有几个？
• 。。。

而我们知道，发问的答案也是不严格递减的，因此使用二分就应该被想到。我们不断发问直到问到小于 x 的有 k - 1 个即可。然而这样的发问也有问题。原因有两个：

1. 小于 x 的有 k - 1 个的数可能不止一个
2. 我们无法确定小于 x 的有 k - 1 个的数一定存在。 比如数对差分别为 [1,1,1,1,2]，让你求第 3 大的，那么小于 x 有两个的数根本就不存在。

我们的思路可调整为求小于等于 x 有 k 个的，接下来我们使用二分法的最左模板即可解决。关于最左模板可参考我的二分查找专题

代码：

class Solution:
    def smallestDistancePair(self, A: List[int], K: int) -> int:
        A.sort()
        l, r = 0, A[-1] - A[0]

        def count_ngt(mid):
            slow = 0
            ans = 0
            for fast in range(len(A)):
                while A[fast] - A[slow] > mid:
                    slow += 1
                ans += fast - slow
            return ans

        while l <= r:
            mid = (l + r) // 2
            if count_ngt(mid) >= K:
                r = mid - 1
            else:
                l = mid + 1
        return l

(代码 1.3.7)

632. 最小区间

题目描述

你有 k 个 非递减排列 的整数列表。找到一个 最小 区间，使得 k 个列表中的每个列表至少有一个数包含在其中。

我们定义如果 b-a < d-c 或者在 b-a == d-c 时 a < c，则区间 [a,b] 比 [c,d] 小。

 

示例 1：

输入：nums = [[4,10,15,24,26], [0,9,12,20], [5,18,22,30]]
输出：[20,24]
解释：
列表 1：[4, 10, 15, 24, 26]，24 在区间 [20,24] 中。
列表 2：[0, 9, 12, 20]，20 在区间 [20,24] 中。
列表 3：[5, 18, 22, 30]，22 在区间 [20,24] 中。
示例 2：

输入：nums = [[1,2,3],[1,2,3],[1,2,3]]
输出：[1,1]
示例 3：

输入：nums = [[10,10],[11,11]]
输出：[10,11]
示例 4：

输入：nums = [[10],[11]]
输出：[10,11]
示例 5：

输入：nums = [[1],[2],[3],[4],[5],[6],[7]]
输出：[1,7]
 

提示：

nums.length == k
1 <= k <= 3500
1 <= nums[i].length <= 50
-105 <= nums[i][j] <= 105
nums[i] 按非递减顺序排列

思路

这道题本质上就是在 m 个一维数组中各取出一个数字，重新组成新的数组 A，使得新的数组 A 中最大值和最小值的差值（diff）最小。

这道题和上面的题目有点类似，又略有不同。这道题是一个矩阵，上面一道题是一维数组。不过我们可以将二维矩阵看出一维数组，这样我们就可以沿用上面的思路了。

上面的思路 diff 最小的一定产生于排序之后相邻的元素之间。而这道题我们无法直接对二维数组进行排序，而且即使进行排序，也不好确定排序的原则。

我们其实可以继续使用前面两道题的思路。具体来说就是使用小顶堆获取堆中最小值，进而通过一个变量记录堆中的最大值，这样就知道了 diff，每次更新指针都会产生一个新的 diff，不断重复这个过程并维护全局最小 diff 即可。

这种算法的成立的前提是 k 个列表都是升序排列的，这里需要数组升序原理和上面题目是一样的，有序之后就可以对每个列表维护一个指针，进而使用上面的思路解决。

以题目中的 nums = [[1,2,3],[1,2,3],[1,2,3]] 为例：

• [1,2,3]
• [1,2,3]
• [1,2,3]

我们先选取所有行的最小值，也就是 [1,1,1]，这时的 diff 为 0，全局最大值为 1，最小值也为 1。接下来，继续寻找备胎，看有没有更好的备胎供我们选择。

接下来的备胎可能产生于情况 1：

• [1,2,3]
• [1,2,3]
• [1,2,3] 移动了这行的指针，将其从原来的 0 移动一个单位到达 1。

或者情况 2：

• [1,2,3]
• [1,2,3]移动了这行的指针，将其从原来的 0 移动一个单位到达 1。
• [1,2,3]

。。。

这几种情况又继续分裂更多的情况，这个就和上面的题目一样了，不再赘述。

代码

class Solution:
    def smallestRange(self, martrix: List[List[int]]) -> List[int]:
        l, r = -10**9, 10**9
        # 将每一行最小的都放到堆中，同时记录其所在的行号和列号，一共 n 个齐头并进
        h = [(row[0], i, 0) for i, row in enumerate(martrix)]
        heapq.heapify(h)
        # 维护最大值
        max_v = max(row[0] for row in martrix)

        while True:
            min_v, row, col = heapq.heappop(h)
            # max_v - min_v 是当前的最大最小差值， r - l 为全局的最大最小差值。因为如果当前的更小，我们就更新全局结果
            if max_v - min_v < r - l:
                l, r = min_v, max_v
            if col == len(martrix[row]) - 1: return [l, r]
            # 更新指针，继续往后移动一位
            heapq.heappush(h, (martrix[row][col + 1], row, col + 1))
            max_v = max(max_v, martrix[row][col + 1])

(代码 1.3.8)

1675. 数组的最小偏移量

题目描述

给你一个由 n 个正整数组成的数组 nums 。

你可以对数组的任意元素执行任意次数的两类操作：

如果元素是 偶数 ，除以 2
例如，如果数组是 [1,2,3,4] ，那么你可以对最后一个元素执行此操作，使其变成 [1,2,3,2]
如果元素是 奇数 ，乘上 2
例如，如果数组是 [1,2,3,4] ，那么你可以对第一个元素执行此操作，使其变成 [2,2,3,4]
数组的 偏移量 是数组中任意两个元素之间的 最大差值 。

返回数组在执行某些操作之后可以拥有的 最小偏移量 。

示例 1：

输入：nums = [1,2,3,4]
输出：1
解释：你可以将数组转换为 [1,2,3,2]，然后转换成 [2,2,3,2]，偏移量是 3 - 2 = 1
示例 2：

输入：nums = [4,1,5,20,3]
输出：3
解释：两次操作后，你可以将数组转换为 [4,2,5,5,3]，偏移量是 5 - 2 = 3
示例 3：

输入：nums = [2,10,8]
输出：3

提示：

n == nums.length
2 <= n <= 105
1 <= nums[i] <= 109

思路

题目说可对数组中每一项都执行任意次操作，但其实操作是有限的。

• 我们只能对奇数进行一次 2 倍操作，因为 2 倍之后其就变成了偶数了。
• 我们可以对偶数进行若干次除 2 操作，直到等于一个奇数，不难看出这也是一个有限次的操作。

以题目中的 [1,2,3,4] 来说。我们可以：

• 将 1 变成 2（也可以不变）
• 将 2 变成 1（也可以不变）
• 将 3 变成 6（也可以不变）
• 将 4 变成 2 或 1（也可以不变）

用图来表示就是下面这样的：

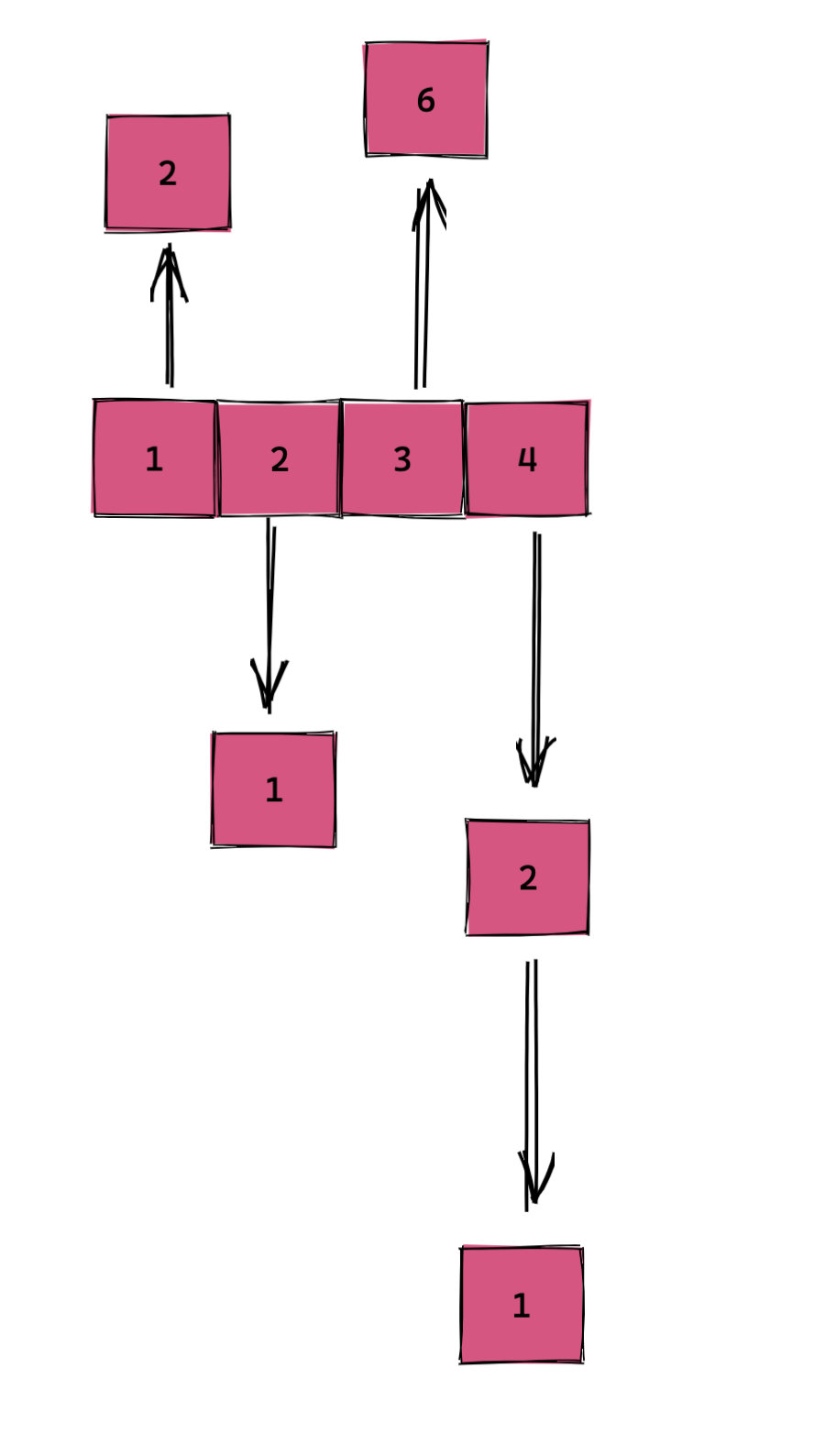
这不就相当于: 从 [[1,2], [1,2], [3,6], [1,2,4]] 这样的一个二维数组中的每一行分别选取一个数，并使得其差最小么？这难道不是和上面的题目一模一样么？

这里我直接将上面的题目解法封装成了一个 api 调用了，具体看代码。

代码

class Solution:
    def smallestRange(self, martrix: List[List[int]]) -> List[int]:
        l, r = -10**9, 10**9
        # 将每一行最小的都放到堆中，同时记录其所在的行号和列号，一共 n 个齐头并进
        h = [(row[0], i, 0) for i, row in enumerate(martrix)]
        heapq.heapify(h)
        # 维护最大值
        max_v = max(row[0] for row in martrix)

        while True:
            min_v, row, col = heapq.heappop(h)
            # max_v - min_v 是当前的最大最小差值， r - l 为全局的最大最小差值。因为如果当前的更小，我们就更新全局结果
            if max_v - min_v < r - l:
                l, r = min_v, max_v
            if col == len(martrix[row]) - 1: return [l, r]
            # 更新指针，继续往后移动一位
            heapq.heappush(h, (martrix[row][col + 1], row, col + 1))
            max_v = max(max_v, martrix[row][col + 1])
    def minimumDeviation(self, nums: List[int]) -> int:
        matrix = [[] for _ in range(len(nums))]
        for i, num in enumerate(nums):
            if num & 1 == 1:
                matrix[i] += [num, num * 2]
            else:
                temp = []
                while num and num & 1 == 0:
                    temp += [num]
                    num //= 2
                temp += [num]
                matrix[i] += temp[::-1]
        a, b = self.smallestRange(matrix)
        return b - a

(代码 1.3.9)

技巧三 - 事后小诸葛

这个技巧指的是：当从左到右遍历的时候，我们是不知道右边是什么的，需要等到你到了右边之后才知道。

如果想知道右边是什么，一种简单的方式是遍历两次，第一次遍历将数据记录下来，当第二次遍历的时候，用上次遍历记录的数据。这是我们使用最多的方式。不过有时候，我们也可以在遍历到指定元素后，往前回溯，这样就可以边遍历边存储，使用一次遍历即可。具体来说就是将从左到右的数据全部收集起来，等到需要用的时候，从里面挑一个用。如果我们都要取最大值或者最小值且极值会发生变动， 就可使用堆加速。直观上就是使用了时光机回到之前，达到了事后诸葛亮的目的。

这样说你肯定不明白啥意思。没关系，我们通过几个例子来讲一下。当你看完这些例子之后，再回头看这句话。

871. 最低加油次数

题目描述

汽车从起点出发驶向目的地，该目的地位于出发位置东面 target 英里处。

沿途有加油站，每个 station[i] 代表一个加油站，它位于出发位置东面 station[i][0] 英里处，并且有 station[i][1] 升汽油。

假设汽车油箱的容量是无限的，其中最初有 startFuel 升燃料。它每行驶 1 英里就会用掉 1 升汽油。

当汽车到达加油站时，它可能停下来加油，将所有汽油从加油站转移到汽车中。

为了到达目的地，汽车所必要的最低加油次数是多少？如果无法到达目的地，则返回 -1 。

注意：如果汽车到达加油站时剩余燃料为 0，它仍然可以在那里加油。如果汽车到达目的地时剩余燃料为 0，仍然认为它已经到达目的地。

 

示例 1：

输入：target = 1, startFuel = 1, stations = []
输出：0
解释：我们可以在不加油的情况下到达目的地。
示例 2：

输入：target = 100, startFuel = 1, stations = [[10,100]]
输出：-1
解释：我们无法抵达目的地，甚至无法到达第一个加油站。
示例 3：

输入：target = 100, startFuel = 10, stations = [[10,60],[20,30],[30,30],[60,40]]
输出：2
解释：
我们出发时有 10 升燃料。
我们开车来到距起点 10 英里处的加油站，消耗 10 升燃料。将汽油从 0 升加到 60 升。
然后，我们从 10 英里处的加油站开到 60 英里处的加油站（消耗 50 升燃料），
并将汽油从 10 升加到 50 升。然后我们开车抵达目的地。
我们沿途在1两个加油站停靠，所以返回 2 。
 

提示：

1 <= target, startFuel, stations[i][1] <= 10^9
0 <= stations.length <= 500
0 < stations[0][0] < stations[1][0] < ... < stations[stations.length-1][0] < target

思路

为了能够获得最低加油次数，我们肯定希望能不加油就不加油。那什么时候必须加油呢？答案应该是如果你不加油，就无法到达下一个目的地的时候。

伪代码描述就是：

cur = startFuel # 刚开始有 startFuel 升汽油
last = 0 # 上一次的位置
for i, fuel in stations:
    cur -= i - last # 走过两个 staton 的耗油为两个 station 的距离，也就是 i - last
    if cur < 0:
        # 我们必须在前面就加油，否则到不了这里
        # 但是在前面的哪个 station 加油呢？
        # 直觉告诉我们应该贪心地选择可以加汽油最多的站 i，如果加上 i 的汽油还是 cur < 0，继续加次大的站 j，直到没有更多汽油可加或者 cur > 0

上面说了要选择可以加汽油最多的站 i，如果加了油还不行，继续选择第二多的站。这种动态求极值的场景非常适合使用 heap。

具体来说就是：

• 每经过一个站，就将其油量加到堆。
• 尽可能往前开，油只要不小于 0 就继续开。
• 如果油量小于 0 ，就从堆中取最大的加到油箱中去，如果油量还是小于 0 继续重复取堆中的最大油量。
• 如果加完油之后油量大于 0 ，继续开，重复上面的步骤。否则返回 -1，表示无法到达目的地。

那这个算法是如何体现事后小诸葛的呢？你可以把自己代入到题目中进行模拟。 把自己想象成正在开车，你的目标就是题目中的要求：最少加油次数。当你开到一个站的时候，你是不知道你的油量够不够支撑到下个站的，并且就算撑不到下个站，其实也许在上个站加油会更好。所以现实中你无论如何都无法知道在当前站，我是应该加油还是不加油的，因为信息太少了。

那我会怎么做呢？如果是我在开车的话，我只能每次都加油，这样都无法到达目的地，那肯定就无法到达目的地了。但如果这样可以到达目的地，我就可以说如果我们在那个站加油，这个站选择不加就可以最少加油次数到达目的地了。你怎么不早说呢？ 这不就是事后诸葛亮么？

这个事后诸葛亮体现在我们是等到没油了才去想应该在之前的某个站加油。

所以这个事后诸葛亮本质上解决的是，基于当前信息无法获取最优解，我们必须掌握全部信息之后回溯。以这道题来说，我们可以先遍历一边 station，然后将每个 station 的油量记录到一个数组中，每次我们“预见“到无法到达下个站的时候，就从这个数组中取最大的。。。。 基于此，我们可以考虑使用堆优化取极值的过程，而不是使用数组的方式。

代码

class Solution:
    def minRefuelStops(self, target: int, startFuel: int, stations: List[List[int]]) -> int:
        stations += [(target, 0)]
        cur = startFuel
        ans = 0

        h = []
        last = 0
        for i, fuel in stations:
            cur -= i - last
            while cur < 0 and h:
                cur -= heapq.heappop(h)
                ans += 1
            if cur < 0:
                return -1
            heappush(h, -fuel)

            last = i
        return ans

(代码 1.3.10)

1488. 避免洪水泛滥

题目描述

你的国家有无数个湖泊，所有湖泊一开始都是空的。当第 n 个湖泊下雨的时候，如果第 n 个湖泊是空的，那么它就会装满水，否则这个湖泊会发生洪水。你的目标是避免任意一个湖泊发生洪水。

给你一个整数数组 rains ，其中：

rains[i] > 0 表示第 i 天时，第 rains[i] 个湖泊会下雨。
rains[i] == 0 表示第 i 天没有湖泊会下雨，你可以选择 一个 湖泊并 抽干 这个湖泊的水。
请返回一个数组 ans ，满足：

ans.length == rains.length
如果 rains[i] > 0 ，那么ans[i] == -1 。
如果 rains[i] == 0 ，ans[i] 是你第 i 天选择抽干的湖泊。
如果有多种可行解，请返回它们中的 任意一个 。如果没办法阻止洪水，请返回一个 空的数组 。

请注意，如果你选择抽干一个装满水的湖泊，它会变成一个空的湖泊。但如果你选择抽干一个空的湖泊，那么将无事发生（详情请看示例 4）。

 

示例 1：

输入：rains = [1,2,3,4]
输出：[-1,-1,-1,-1]
解释：第一天后，装满水的湖泊包括 [1]
第二天后，装满水的湖泊包括 [1,2]
第三天后，装满水的湖泊包括 [1,2,3]
第四天后，装满水的湖泊包括 [1,2,3,4]
没有哪一天你可以抽干任何湖泊的水，也没有湖泊会发生洪水。
示例 2：

输入：rains = [1,2,0,0,2,1]
输出：[-1,-1,2,1,-1,-1]
解释：第一天后，装满水的湖泊包括 [1]
第二天后，装满水的湖泊包括 [1,2]
第三天后，我们抽干湖泊 2 。所以剩下装满水的湖泊包括 [1]
第四天后，我们抽干湖泊 1 。所以暂时没有装满水的湖泊了。
第五天后，装满水的湖泊包括 [2]。
第六天后，装满水的湖泊包括 [1,2]。
可以看出，这个方案下不会有洪水发生。同时， [-1,-1,1,2,-1,-1] 也是另一个可行的没有洪水的方案。
示例 3：

输入：rains = [1,2,0,1,2]
输出：[]
解释：第二天后，装满水的湖泊包括 [1,2]。我们可以在第三天抽干一个湖泊的水。
但第三天后，湖泊 1 和 2 都会再次下雨，所以不管我们第三天抽干哪个湖泊的水，另一个湖泊都会发生洪水。
示例 4：

输入：rains = [69,0,0,0,69]
输出：[-1,69,1,1,-1]
解释：任何形如 [-1,69,x,y,-1], [-1,x,69,y,-1] 或者 [-1,x,y,69,-1] 都是可行的解，其中 1 <= x,y <= 10^9
示例 5：

输入：rains = [10,20,20]
输出：[]
解释：由于湖泊 20 会连续下 2 天的雨，所以没有没有办法阻止洪水。
 

提示：

1 <= rains.length <= 10^5
0 <= rains[i] <= 10^9

思路

如果上面的题用事后诸葛亮描述比较牵强的话，那后面这两个题可以说很适合了。

题目说明了我们可以在不下雨的时候抽干一个湖泊，如果有多个下满雨的湖泊，我们该抽干哪个湖呢？显然应该是抽干最近即将被洪水淹没的湖。但是现实中无论如何我们都不可能知道未来哪天哪个湖泊会下雨的，即使有天气预报也不行，因此它也不 100% 可靠。

但是代码可以啊。我们可以先遍历一遍 rain 数组就知道第几天哪个湖泊下雨了。有了这个信息，我们就可以事后诸葛亮了。

“今天天气很好，我开了天眼，明天湖泊 2 会被洪水淹没，我们今天就先抽干它，否则就洪水泛滥了。”。

和上面的题目一样，我们也可以不先遍历 rain 数组，再模拟每天的变化，而是直接模拟，即使当前是晴天我们也不抽干任何湖泊。接着在模拟的过程记录晴天的情况，等到洪水发生的时候，我们再考虑前面哪一个晴天应该抽干哪个湖泊。因此这个事后诸葛亮体现在我们是等到洪水泛滥了才去想应该在之前的某天采取什么手段。

算法：

• 遍历 rain， 模拟每天的变化
• 如果 rain 当前是 0 表示当前是晴天，我们不抽干任何湖泊。但是我们将当前天记录到 sunny 数组。
• 如果 rain 大于 0，说明有一个湖泊下雨了，我们去看下下雨的这个湖泊是否发生了洪水泛滥。其实就是看下下雨前是否已经有水了。这提示我们用一个数据结构 lakes 记录每个湖泊的情况，我们可以用 0 表示没有水，1 表示有水。这样当湖泊 i 下雨的时候且 lakes[i] = 1 就会发生洪水泛滥。
• 如果当前湖泊发生了洪水泛滥，那么就去 sunny 数组找一个晴天去抽干它，这样它就不会洪水泛滥，接下来只需要保持 lakes[i] = 1 即可。

这道题没有使用到堆，我是故意的。之所以这么做，是让大家明白事后诸葛亮这个技巧并不是堆特有的，实际上这就是一种普通的算法思想，就好像从后往前遍历一样。只不过，很多时候，我们事后诸葛亮的场景，需要动态取最大最小值， 这个时候就应该考虑使用堆了，这其实又回到文章开头的一个中心了，所以大家一定要灵活使用这些技巧，不可生搬硬套。

下一道题是一个不折不扣的事后诸葛亮 + 堆优化的题目。

代码

class Solution:
    def avoidFlood(self, rains: List[int]) -> List[int]:
        ans = [1] * len(rains)
        lakes = collections.defaultdict(int)
        sunny = []

        for i, rain in enumerate(rains):
            if rain > 0:
                ans[i] = -1
                if lakes[rain - 1] == 1:
                    if 0 == len(sunny):
                        return []
                    ans[sunny.pop()] = rain
                lakes[rain - 1] = 1
            else:
                sunny.append(i)
        return ans

(代码 1.3.11)

2021-04-06 fixed: 上面的代码有问题。错误的原因在于上述算法如果当前湖泊发生了洪水泛滥，那么就去 sunny 数组找一个晴天去抽干它，这样它就不会洪水泛滥部分的实现不对。sunny 数组找一个晴天去抽干它的根本前提是 出现晴天的时候湖泊里面要有水才能抽，如果晴天的时候，湖泊里面没有水也不行。这提示我们的 lakes 不存储 0 和 1 ，而是存储发生洪水是第几天。这样问题就变为在 sunny 中找一个日期大于 lakes[rain-1] 的项，并将其移除 sunny 数组。由于 sunny 数组是有序的，因此我们可以使用二分来进行查找。

由于我们需要删除 sunny 数组的项，因此时间复杂度不会因为使用了二分而降低。

正确的代码应该为：

class Solution:
    def avoidFlood(self, rains: List[int]) -> List[int]:
        ans = [1] * len(rains)
        lakes = {}
        sunny = []

        for i, rain in enumerate(rains):
            if rain > 0:
                ans[i] = -1
                if rain - 1 in lakes:
                    j = bisect.bisect_left(sunny, lakes[rain - 1])
                    if j == len(sunny):
                        return []
                    ans[sunny.pop(j)] = rain
                lakes[rain - 1] = i
            else:
                sunny.append(i)
        return ans

1642. 可以到达的最远建筑

题目描述

给你一个整数数组 heights ，表示建筑物的高度。另有一些砖块 bricks 和梯子 ladders 。

你从建筑物 0 开始旅程，不断向后面的建筑物移动，期间可能会用到砖块或梯子。

当从建筑物 i 移动到建筑物 i+1（下标 从 0 开始 ）时：

如果当前建筑物的高度 大于或等于 下一建筑物的高度，则不需要梯子或砖块
如果当前建筑的高度 小于 下一个建筑的高度，您可以使用 一架梯子 或 (h[i+1] - h[i]) 个砖块
如果以最佳方式使用给定的梯子和砖块，返回你可以到达的最远建筑物的下标（下标 从 0 开始 ）。

示例 1：


输入：heights = [4,2,7,6,9,14,12], bricks = 5, ladders = 1
输出：4
解释：从建筑物 0 出发，你可以按此方案完成旅程：
- 不使用砖块或梯子到达建筑物 1 ，因为 4 >= 2
- 使用 5 个砖块到达建筑物 2 。你必须使用砖块或梯子，因为 2 < 7
- 不使用砖块或梯子到达建筑物 3 ，因为 7 >= 6
- 使用唯一的梯子到达建筑物 4 。你必须使用砖块或梯子，因为 6 < 9
无法越过建筑物 4 ，因为没有更多砖块或梯子。
示例 2：

输入：heights = [4,12,2,7,3,18,20,3,19], bricks = 10, ladders = 2
输出：7
示例 3：

输入：heights = [14,3,19,3], bricks = 17, ladders = 0
输出：3
 

提示：

1 <= heights.length <= 105
1 <= heights[i] <= 106
0 <= bricks <= 109
0 <= ladders <= heights.length

思路

我们可以将梯子看出是无限的砖块，只不过只能使用一次，我们当然希望能将好梯用在刀刃上。和上面一样，如果是现实生活，我们是无法知道啥时候用梯子好，啥时候用砖头好的。

没关系，我们继续使用事后诸葛亮法，一次遍历就可完成。和前面的思路类似，那就是我无脑用梯子，等梯子不够用了，我们就要开始事后诸葛亮了，要是前面用砖头就好了。那什么时候用砖头就好了呢？很明显就是当初用梯子的时候高度差，比现在的高度差小。

直白点就是当初我用梯子爬了个 5 米的墙，现在这里有个十米的墙，我没梯子了，只能用 10 个砖头了。要是之前用 5 个砖头，现在不就可以用一个梯子，从而省下 5 个砖头了吗？

这提示我们将用前面用梯子跨越的建筑物高度差存起来，等到后面梯子用完了，我们将前面被用的梯子“兑换”成砖头继续用。以上面的例子来说，我们就可以先兑换 10 个砖头，然后将 5 个砖头用掉，也就是相当于增加了 5 个砖头。

如果前面多次使用了梯子，我们优先“兑换”哪次呢？显然是优先兑换高度差大的，这样兑换的砖头才最多。这提示每次都从之前存储的高度差中选最大的，并在“兑换”之后将其移除。这种动态求极值的场景用什么数据结构合适？当然是堆啦。

代码

class Solution:
    def furthestBuilding(self, heights: List[int], bricks: int, ladders: int) -> int:
        h = []
        for i in range(1, len(heights)):
            diff = heights[i] - heights[i - 1]
            if diff <= 0:
                continue
            if bricks < diff and ladders > 0:
                ladders -= 1
                if h and -h[0] > diff:
                    bricks -= heapq.heappop(h)
                else:
                    continue
            bricks -= diff
            if bricks < 0:
                return i - 1
            heapq.heappush(h, -diff)
        return len(heights) - 1

(代码 1.3.12)

四大应用

接下来是本文的最后一个部分《四大应用》，目的是通过这几个例子来帮助大家巩固前面的知识。

1. topK

求解 topK 是堆的一个很重要的功能。这个其实已经在前面的固定堆部分给大家介绍过了。

这里直接引用前面的话：

“其实求第 k 小的数最简单的思路是建立小顶堆，将所有的数先全部入堆，然后逐个出堆，一共出堆 k 次。最后一次出堆的就是第 k 小的数。然而，我们也可不先全部入堆，而是建立大顶堆（注意不是上面的小顶堆），并维持堆的大小为 k 个。如果新的数入堆之后堆的大小大于 k，则需要将堆顶的数和新的数进行比较，并将较大的移除。这样可以保证堆中的数是全体数字中最小的 k 个，而这最小的 k 个中最大的（即堆顶）不就是第 k 小的么？这也就是选择建立大顶堆，而不是小顶堆的原因。”

其实除了第 k 小的数，我们也可以将中间的数全部收集起来，这就可以求出最小的 k 个数。和上面第 k 小的数唯一不同的点在于需要收集 popp 出来的所有的数。

需要注意的是，有时候权重并不是原本数组值本身的大小，也可以是距离，出现频率等。

相关题目：

• 面试题 17.14. 最小 K 个数
• 347. 前 K 个高频元素
• 973. 最接近原点的 K 个点

力扣中有关第 k 的题目很多都是堆。除了堆之外，第 k 的题目其实还会有一些找规律的题目，对于这种题目则可以通过分治+递归的方式来解决，具体就不再这里展开了，感兴趣的可以和我留言讨论。

2. 带权最短距离

关于这点，其实我在前面部分也提到过了，只不过当时只是一带而过。原话是“不过 BFS 真的就没人用优先队列实现么？当然不是！比如带权图的最短路径问题，如果用队列做 BFS 那就需要优先队列才可以，因为路径之间是有权重的差异的，这不就是优先队列的设计初衷么。使用优先队列的 BFS 实现典型的就是 dijkstra 算法。”

DIJKSTRA 算法主要解决的是图中任意两点的最短距离。

算法的基本思想是贪心，每次都遍历所有邻居，并从中找到距离最小的，本质上是一种广度优先遍历。这里我们借助堆这种数据结构，使得可以在 $logN$ 的时间内找到 cost 最小的点，其中 N 为 堆的大小。

代码模板：

def dijkstra(graph, start, end):
    # 堆里的数据都是 (cost, i) 的二元祖，其含义是“从 start 走到 i 的距离是 cost”。
    heap = [(0, start)]
    visited = set()
    while heap:
        (cost, u) = heapq.heappop(heap)
        if u in visited:
            continue
        visited.add(u)
        if u == end:
            return cost
        for v, c in graph[u]:
            if v in visited:
                continue
            next = cost + c
            heapq.heappush(heap, (next, v))
    return -1

(代码 1.4.1)

可以看出代码模板和 BFS 基本是类似的。如果你自己将堆的 key 设定为 steps 也可模拟实现 BFS，这个在前面已经讲过了，这里不再赘述。

比如一个图是这样的：

E -- 1 --> B -- 1 --> C -- 1 --> D -- 1 --> F
 \                                         /\
  \                                        ||
    -------- 2 ---------> G ------- 1 ------

我们使用邻接矩阵来构造：

G = {
    "B": [["C", 1]],
    "C": [["D", 1]],
    "D": [["F", 1]],
    "E": [["B", 1], ["G", 2]],
    "F": [],
    "G": [["F", 1]],
}

shortDistance = dijkstra(G, "E", "C")
print(shortDistance)  # E -- 3 --> F -- 3 --> C == 6

会了这个算法模板， 你就可以去 AC 743. 网络延迟时间 了。

完整代码：

class Solution:
    def dijkstra(self, graph, start, end):
        heap = [(0, start)]
        visited = set()
        while heap:
            (cost, u) = heapq.heappop(heap)
            if u in visited:
                continue
            visited.add(u)
            if u == end:
                return cost
            for v, c in graph[u]:
                if v in visited:
                    continue
                next = cost + c
                heapq.heappush(heap, (next, v))
        return -1
    def networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:
        graph = collections.defaultdict(list)
        for fr, to, w in times:
            graph[fr - 1].append((to - 1, w))
        ans = -1
        for to in range(N):
            # 调用封装好的 dijkstra 方法
            dist = self.dijkstra(graph, K - 1, to)
            if dist == -1: return -1
            ans = max(ans, dist)
        return ans

(代码 1.4.2)

你学会了么？

上面的算法并不是最优解，我只是为了体现将 dijkstra 封装为 api 调用 的思想。一个更好的做法是一次遍历记录所有的距离信息，而不是每次都重复计算。时间复杂度会大大降低。这在计算一个点到图中所有点的距离时有很大的意义。 为了实现这个目的，我们的算法会有什么样的调整？

提示：你可以使用一个 dist 哈希表记录开始点到每个点的最短距离来完成。想出来的话，可以用力扣 882 题去验证一下哦~

其实只需要做一个小的调整就可以了，由于调整很小，直接看代码会比较好。

代码：

class Solution:
    def dijkstra(self, graph, start, end):
        heap = [(0, start)]  # cost from start node,end node
        dist = {}
        while heap:
            (cost, u) = heapq.heappop(heap)
            if u in dist:
                continue
            dist[u] = cost
            for v, c in graph[u]:
                if v in dist:
                    continue
                next = cost + c
                heapq.heappush(heap, (next, v))
        return dist
    def networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:
        graph = collections.defaultdict(list)
        for fr, to, w in times:
            graph[fr - 1].append((to - 1, w))
        ans = -1
        dist = self.dijkstra(graph, K - 1, to)
        return -1 if len(dist) != N else max(dist.values())

(代码 1.4.3)

可以看出我们只是将 visitd 替换成了 dist，其他不变。另外 dist 其实只是带了 key 的 visited，它这里也起到了 visitd 的作用。

如果你需要计算一个节点到其他所有节点的最短路径，可以使用一个 dist （一个 hashmap）来记录出发点到所有点的最短路径信息，而不是使用 visited （一个 hashset）。

类似的题目也不少， 我再举一个给大家 787. K 站中转内最便宜的航班。题目描述：

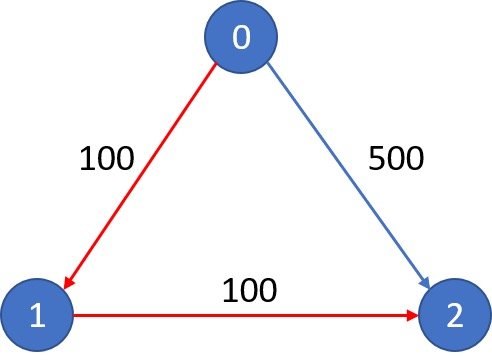
有 n 个城市通过 m 个航班连接。每个航班都从城市 u 开始，以价格 w 抵达 v。

现在给定所有的城市和航班，以及出发城市 src 和目的地 dst，你的任务是找到从 src 到 dst 最多经过 k 站中转的最便宜的价格。 如果没有这样的路线，则输出 -1。

 

示例 1：

输入:
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 1
输出: 200
解释:
城市航班图如下

从城市 0 到城市 2 在 1 站中转以内的最便宜价格是 200，如图中红色所示。
示例 2：

输入:
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 0
输出: 500
解释:
城市航班图如下

从城市 0 到城市 2 在 0 站中转以内的最便宜价格是 500，如图中蓝色所示。
 

提示：

n 范围是 [1, 100]，城市标签从 0 到 n - 1
航班数量范围是 [0, n * (n - 1) / 2]
每个航班的格式 (src, dst, price)
每个航班的价格范围是 [1, 10000]
k 范围是 [0, n - 1]
航班没有重复，且不存在自环

这道题和上面的没有本质不同， 我仍然将其封装成 API 来使用，具体看代码就行。

这道题唯一特别的点在于如果中转次数大于 k，也认为无法到达。这个其实很容易，我们只需要在堆中用元组来多携带一个 steps即可，这个 steps 就是 不带权 BFS 中的距离。如果 pop 出来 steps 大于 K，则认为非法，我们跳过继续处理即可。

class Solution:
    # 改造一下，增加参数 K，堆多携带一个 steps 即可
    def dijkstra(self, graph, start, end, K):
        heap = [(0, start, 0)]
        visited = set()
        while heap:
            (cost, u, steps) = heapq.heappop(heap)
            if u in visited:
                continue
            visited.add((u, steps))
            if steps > K: continue
            if u == end:
                return cost
            for v, c in graph[u]:
                if (v, steps) in visited:
                    continue
                next = cost + c
                heapq.heappush(heap, (next, v, steps + 1))
        return -1
    def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, K: int) -> int:
        graph = collections.defaultdict(list)
        for fr, to, price in flights:
            graph[fr].append((to, price))
         # 调用封装好的 dijkstra 方法
        return self.dijkstra(graph, src, dst, K + 1)

(代码 1.4.4)

3. 因子分解

和上面两个应用一下，这个我在前面 《313. 超级丑数》部分也提到了。

回顾一下丑数的定义： 丑数就是质因数只包含 2, 3, 5 的正整数。 因此丑数本质就是一个数经过因子分解之后只剩下 2，3，5 的整数，而不携带别的因子了。

关于丑数的题目有很多，大多数也可以从堆的角度考虑来解。只不过有时候因子个数有限，不使用堆也容易解决。比如：264. 丑数 II 就可以使用三个指针来记录即可，这个技巧在前面也讲过了，不再赘述。

一些题目并不是丑数，但是却明确提到了类似因子的信息，并让你求第 k 大的 xx，这个时候优先考虑使用堆来解决。如果题目中夹杂一些其他信息，比如有序，则也可考虑二分法。具体使用哪种方法，要具体问题具体分析，不过在此之前大家要对这两种方法都足够熟悉才行。

4. 堆排序

前面的三种应用或多或少在前面都提到过。而堆排序却未曾在前面提到。

直接考察堆排序的题目几乎没有。但是面试却有可能会考察，另外学习堆排序对你理解分治等重要算法思维都有重要意义。个人感觉，堆排序，构造二叉树，构造线段树等算法都有很大的相似性，掌握一种，其他都可以触类旁通。

实际上，经过前面的堆的学习，我们可以封装一个堆排序，方法非常简单。

这里我放一个使用堆的 api 实现堆排序的简单的示例代码：

h = [9,5,2,7]
heapq.heapify(h)
ans = []

while h:
    ans.append(heapq.heappop(h))
print(ans) # 2,5,7,9

明白了示例， 那封装成通用堆排序就不难了。

def heap_sort(h):
    heapq.heapify(h)
    ans = []
    while h:
        ans.append(heapq.heappop(h))
    return ans

这个方法足够简单，如果你明白了前面堆的原理，让你手撸一个堆排序也不难。可是这种方法有个弊端，它不是原位算法，也就是说你必须使用额外的空间承接结果，空间复杂度为 $O(N)$。但是其实调用完堆排序的方法后，原有的数组内存可以被释放了，因此理论上来说空间也没浪费，只不过我们计算空间复杂度的时候取的是使用内存最多的时刻，因此使用原地算法毫无疑问更优秀。如果你实在觉得不爽这个实现，也可以采用原地的修改的方式。这倒也不难，只不过稍微改造一下前面的堆的实现即可，由于篇幅的限制，这里不多讲了。

总结

堆和队列有千丝万缕的联系。 很多题目我都是先思考使用堆来完成。然后发现每次入堆都是 + 1，而不会跳着更新，比如下一个是 + 2，+3 等等，因此使用队列来完成性能更好。 比如 649. Dota2 参议院 和 1654. 到家的最少跳跃次数 等。

堆的中心就一个，那就是动态求极值。

而求极值无非就是最大值或者最小值，这不难看出。如果求最大值，我们可以使用大顶堆，如果求最小值，可以用最小堆。而实际上，如果没有动态两个字，很多情况下没有必要使用堆。比如可以直接一次遍历找出最大的即可。而动态这个点不容易看出来，这正是题目的难点。这需要你先对问题进行分析， 分析出这道题其实就是动态求极值，那么使用堆来优化就应该被想到。

堆的实现有很多。比如基于链表的跳表，基于数组的二叉堆和基于红黑树的实现等。这里我们介绍了两种主要实现 并详细地讲述了二叉堆的实现，不仅是其实现简单，而且其在很多情况下表现都不错，推荐大家重点掌握二叉堆实现。

对于二叉堆的实现，核心点就一点，那就是始终维护堆的性质不变，具体是什么性质呢？那就是 父节点的权值不大于儿子的权值（小顶堆）。为了达到这个目的，我们需要在入堆和出堆的时候，使用上浮和下沉操作，并恰当地完成元素交换。具体来说就是上浮过程和比它大的父节点进行交换，下沉过程和两个子节点中较小的进行交换，当然前提是它有子节点且子节点比它小。

关于堆化我们并没有做详细分析。不过如果你理解了本文的入堆操作，这其实很容易。因此堆化本身就是一个不断入堆的过程，只不过将时间上的离散的操作变成了一次性操作而已。

另外我给大家介绍了三个堆的做题技巧，分别是：

• 固定堆，不仅可以解决第 k 问题，还可有效利用已经计算的结果，避免重复计算。
• 多路归并，本质就是一个暴力解法，和暴力递归没有本质区别。如果你将其转化为递归，也是一种不能记忆化的递归。因此更像是回溯算法。
• 事后小诸葛。有些信息，我们在当前没有办法获取，就可用一种数据结构存起来，方便之后”东窗事发“的时候查。这种数据解决可以是很多，常见的有哈希表和堆。你也可以将这个技巧看成是事后后悔，有的人比较能接受这种叫法，不过不管叫法如何，指的都是这个含义。

最后给大家介绍了四种应用，这四种应用除了堆排序，其他在前面或多或少都讲过，它们分别是：

• topK
• 带权最短路径
• 因子分解
• 堆排序

这四种应用实际上还是围绕了堆的一个中心动态取极值，这四种应用只不过是灵活使用了这个特点罢了。因此大家在做题的时候只要死记动态求极值即可。如果你能够分析出这道题和动态取极值有关，那么请务必考虑堆。接下来我们就要在脑子中过一下复杂度，对照一下题目数据范围就大概可以估算出是否可行啦。

大家对此有何看法，欢迎给我留言，我有时间都会一一查看回答。更多算法套路可以访问我的 LeetCode 题解仓库：https://github.com/azl397985856/leetcode 。目前已经 39K star 啦。大家也可以关注我的公众号《力扣加加》带你啃下算法这块硬骨头。