lucifer

前两篇的地址在这里，没有看过的同学建议先看下。

本章或许是这个系列的最终章。这次给大家聊一点硬核的，聊一些几乎所有算法题都能用得上的超实用思想。

上一节给大家抛出了两个问题，分别是：

  • 如何锁定使用哪种算法？比如我看到了这道题，我怎么知道该用什么解法呢？二分？动态规划？
  • 一看就会，一写就废， 如何克服？

今天，我就来圆一个当初吹下的牛逼。话不多说，直接上干货。如果你觉得有用，请三连支持我一下，让我能够坚持下去，给大家带来更多的干货。

如何锁定使用哪种算法？

为什么很多人刚看了一眼题目就知道怎么解？

  • 一种可能是 ta 之前做过同样或者类似的题目，形成了内在的记忆，直接提取了之前的记忆。
  • 另一种可能是题目给出了明确的提示信息，他们根据这些信息”蒙“的，这种蒙就是题感。
  • 最后一种是刚开始也没思路，尝试暴力解，发现某些步骤可以优化，慢慢剥茧抽丝，推导出最终答案。

接下来，我们来聊下第二种和第三种。至于第一种则不是一篇文章能解决的，这需要大家多做题，并且做题的时候要多总结多交流。

关键字

关键字可以对解题起到提示作用。这很好理解，假设题目没有限制信息等关键字，那就是耍流氓，毫无算法可言了。 比如”在一个数组中找 target“，这道题就很无聊，正常不会有这种算法题。 可能的出题形式是加上有序两个字，变成有序数组。那有序就是关键字了。

其他的例子有很多，接下来我们来看下常见的关键字以及对应的可能解法有哪些。

  • 如果题目是求极值，计数，很有可能是动态规划，堆等。

  • 如果题目是有序的，则可能是双指针。比如二分法。

  • 如果题目要求连续，则可能是滑动窗口。

  • 如果题目要求所有可能，需要路径信息，则可能是回溯。

如上的这些只是看到关键词你应该第一时间想到的可能解法，究竟正确与否，以及复杂度是否达标需要在脑子里二次加工。

关于复杂度是否达标这一点，后面给大家介绍。

限制条件

很多题目都会给一些数据范围的提示，大家一定要注意看。 比如 1681. 最小不兼容性，题目描述就不看了，我们不打算在这里讲具体怎么解。这道题的函数签名如下：

1
def minimumIncompatibility(self, nums: List[int], k: int) -> int:

这道题的提示是这样的:

1
2
3
1 <= k <= nums.length <= 16
nums.length 能被 k 整除。
1 <= nums[i] <= nums.length

看到了这个你有什么想法么？

注意到 nums 的长度和值都很小，这道题很可能是暴力回溯 + 状态压缩。关于回溯和状态压缩技巧可以翻翻我的历史文章。

这里再给大家一个超实用小技巧。

  • 如果 n 是 10 左右，那么算法通常是 n! 的时间复杂度。
  • 如果 n 是 20 左右，那么算法通常是 2^n 的时间复杂度

因此 1681. 最小不兼容性 这道题的复杂度很可能就是指数级别。

那为什么 10 左右就是 n!，20 是 2^n? 这里给大家介绍一个你可能不知道的技巧。请大家记住一个数字 1000 万。

上面之所以是 10 左右， 20 左右就是因为你把 n 带进去差不多都是 1000 万。 再比如一道题是 n 是 $10^7$，那很可能是$O(N)$复杂度，因为 $10 ^7$ 就是 1000 万。

再比如，我之前写的一篇文章《穿上衣服我就不认识你了？来聊聊最长上升子序列》，上面所有的题时间复杂度都是 $N^2$，基本都可以通过所有的测试用例。为什么？因为题目数据范围差不多是 2500，那 2500 的平方是多少？是 600 多万，因此数据范围是 3000 以内， 平方差不多都可解，当然我说的只是大多数情况，并且需要注意越接近临界值越可能超时。

再比如1631. 最小体力消耗路径。题目描述：

1
2
3
4
5
你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往 上，下，左，右 四个方向之一移动，你想要找到耗费 体力 最小的一条路径。

一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。

请你返回从左上角走到右下角的最小 体力消耗值 。。

示例 1：

1
2
3
4
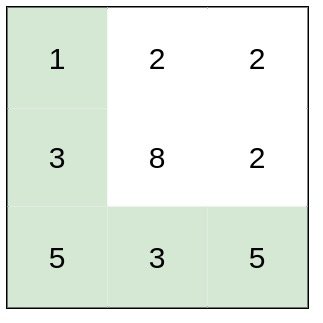
输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。

这道题的函数签名如下：

1
2
class Solution:
    def minimumEffortPath(self, heights: List[List[int]]) -> int:

这道题的提示是这样的:

1
2
3
4
rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
1 <= heights[i][j] <= 10^6

首先，我们至少需要从左上走到右下，那么时间复杂度就已经是 $O(rows * columns)$ 了。题目说了这两个数字都不大于 100，因此最大就是 $10^4$。而对于路线上的高度差绝对值的数据范围也不超过 $10^6$。

暴力法就是一个个试， 复杂度是二者直接相乘，也就是 $10^10$，大于前面给大家讲的 $10^7$，因此这个复杂度通常是不能 AC 的。

而上面说了 $O(rows * columns)$ 是不可能省的，因为你至少要走一次。但如果 $10^6$ 不是线性去试，而是指数的话呢？而指数复杂度首先想到二分。

此题的伪代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def minimumEffortPath(self, heights: List[List[int]]) -> int:
        def test(mid, x, y):
            # dosomething
        l, r = 0, 10**6
        # 最左满足条件的值的二分模板。大家可以去 leetcode-cheatsheet 插件获取更多算法模板
        while l <= r:
            mid = (l + r) // 2
            # 测试有没有一条路径从(0,0)出发到达(rows-1,cols-1)，且路径上的高度绝对值差不大于 mid
            if test(mid, 0, 0):
                r = mid - 1
            else:
                l = mid + 1
        return l

你说 1000 万这个数字重要不重要？1000 万不仅是我的人生目标，更是做题时刻铭记的一个数字！^_^

暴力优化

最后给大家介绍的”识别题目可能的解法“的技巧是暴力优化。

一句话概括就是先暴力解，然后思考性能瓶颈，再尝试使用数据结构和算法对瓶颈进行优化。

比如 316. 去除重复字母，我就是先暴力求出来。发现每次都直接判断是否在是否在栈上需要 $O(N)$ 的时间，太慢了。由于我就用了哈希表进行优化。而使用哈希表这点，绝对不是我一开始就想到的，而是先暴力求解，求解的过程发现算法的性能瓶颈才意识到该用哈希表的。关于这道题的详细的解法就不再这里讲了，大家点进去看我的题解就行。或者直接去力扣搜题，排名第一的非官方题解应该就是我。

总结一下就是，大家一定不要小看暴力法。暴力法解出来剪剪枝说不定就过了。如果不过，思考下瓶颈在哪，用合适的数据结构和算法优化一下说不定也就过了。这可不是随便说说。比如下面要讲的硬币找零问题，就是暴力解发现瓶颈，加个记忆化去除重复子问题就是动态规划了

一看就会，一写就废， 如何克服？

针对这个问题，之前我给大家的建议是多复习， 多动手写。

后来我和几个朋友聊了一下，发现自己有点幸存者偏差。我发现很多人在没有算法思维的情况下就开始学习算法了，这很不可取。

不过算法思维这东西你让我在这一篇文章给你整的明明白白的，这也不现实。今天我给大家分享一个我认为最最重要的一个算法思想 - 分治。

分治思维

“一看就会，一写就废， 如何克服？”，有一个可能是你没有分治思维。 我们的大脑天生适合处理一些简单的东西，而不适合处理看起来就很复杂的东西。因此面对一个很复杂的东西，第一件事情应该是思考是否可以将其分解 ，然后逐个击破。

举个例子给大家，如下是一道力扣的 hard 题 《2 出现的次数》，题目描述如下：

1
2
3
4
5
6
7
8
9
10
编写一个方法，计算从 0 到 n (含 n) 中数字 2 出现的次数。

示例:

输入: 25
输出: 9
解释: (2, 12, 20, 21, 22, 23, 24, 25)(注意 22 应该算作两次)
提示：

n <= 10^9

很多人一看到题就蒙了，这要多少种情况啊? 总不可能一个数字一个数字试过去吧？

其实看一眼数据范围中 n 上限是 10^9，大于 1000 万，就知道不能这样暴力。

于是悄悄打开题解，不仅感叹“原来是这样啊！”，“这怎么想到的？这什么脑子啊！”

来让我告诉你，你缺啥。 你缺的不是一个好使的脑子，而是一个懂得将复杂问题变成若干个简单问题的意识和能力。

以这道题来说， 我可以将其分解为几个子问题。

  • 从 0 到 n (含 n) 中 个位 数字 2 出现的次数
  • 从 0 到 n (含 n) 中 十位 数字 2 出现的次数
  • 。。。

最终的答案就是以上几个子问题的和。

经过这样的思路，大家一下子就能打开思路。剩下的任务就简单了。因为每次固定一位之后，就将数字分为了左右两部分，那么该位是 2 的次数就是左右所有可能的笛卡尔积，即 a * b。

比如 n 是 135。

百位上不可能是 2，因为 2xx 一定超过 135 了。

那十位有多少个 2 呢？按照上面的思路：

  • 左边就是百位，百位可能是 0 或者 1，共 2 种可能。
  • 右边就是个位，个位可能是 [0 - 9] 共 10 种可能。

那么十位是 2 的次数就是 2 * 10 = 20。

那个位有多少个 2 呢？按照上面的思路：

  • 左边就是十位和百位，其可能是 [0-13]，共 14 种可能。
  • 右边啥都没有，1 种可能。

那么个位是 2 的次数就是 14 种。

因此不超过 135 的数字中 2 的出现次数就是 20 + 14 = 34 种。

当然，这里面还有一些细节，比如如果某一位比 2 小或者正好是 2 怎么办？我就不在这里讲了。这里直接贴下代码，大家自己继续完成好了。

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def numberOf2sInRange(self, n: int) -> int:
        ans = 0
        m = 1
        while m <= n:
            cur = n // m % 10
            if cur > 2: ans += (n // m // 10 + 1) * m
            else:
                if cur == 2: ans += n % m + 1
                ans += (n // m // 10) * m
            m *= 10
        return ans

把 2 换成其他数字 x，那就可以计算不超过 n 的 x 的出现次数。

举这个例子就想告诉大家为啥一些题目你压根就没有思路的原因：

  • 要么就是这种题没见过，那没办法，多做题呗。
  • 要么就是你算法思维还不够。比如我上面讲的分治的算法思维。

一看就会又说明这种题你是回答过的，因此一看就会，一写就废，一般都是没有养成良好的算法思维，而分治就是一种非常重要的算法思维。当算法思维有了，剩下的细节就慢慢练习就好了，这没有捷径。但是算法思维是有捷径的，大家在刷题之前要特别注重算法思维的学习。

我再举几个例子给大家，帮助大家加深理解。

三个题目带你理解分治思想

  1. 在一个数组 nums 中找值为 target 的元素，并返回数组下标，题目保证 nums 中有且仅有一个数等于 target。
  2. 给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。你可以认为每种硬币的数量是无限的。（322. 零钱兑换）
  3. n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。（51. N 皇后）

这几道题覆盖了简单中等和困难三种难度。接下来，我们来看下这几个题。

第一题

对于第一题， 答案无非就是 [0, n - 1]。因此我们可以将问题分解为以下几个子问题：

  • 是 0 么？no
  • 是 1 么？no
  • 是 2 么？no
  • 。。。

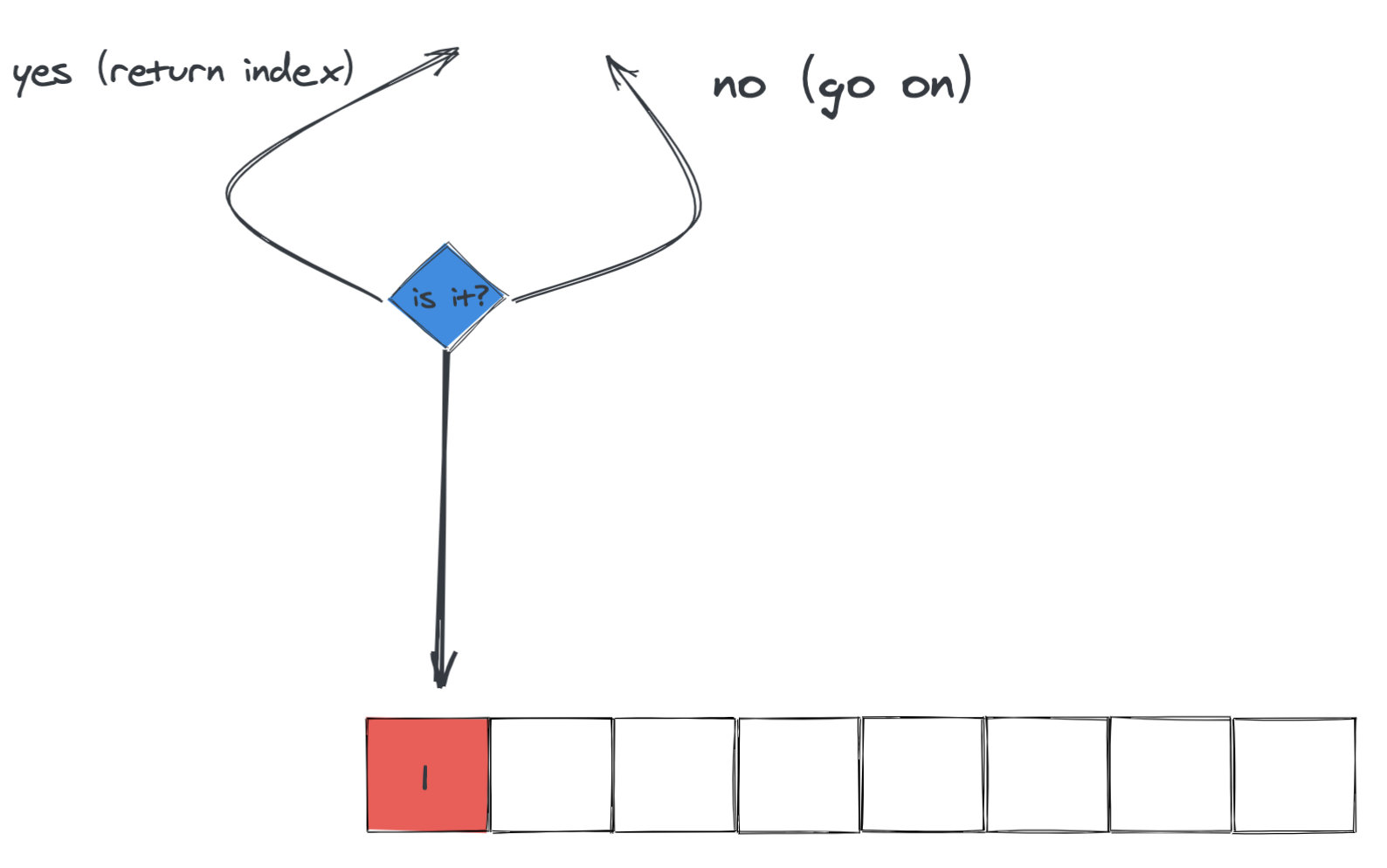
最终的答案就是子问题中回答为 “yes” 的索引。严格意义上来说，这里只有分，没有治，而且这个分和前面的分有微妙的差异。前面的分完之后后面还要用，这个分是直接给扔掉了。类似的有二分法，二分法就是一种只有分没有治的“分治法”。

第二题

coins 是个变量， amount 也是变量，它们关系感觉好多的样子？我该怎么理清呢？

我们从特殊入手，比如 coins = [1, 2, 5], amount = 11。为了方便描述，原问题我用 f([1,2,5], 11) 表示 coins 为 [1,2,5]，amount 为 11 的最少需要多少硬币凑齐。

我也不知道最终的最少硬币方案是怎么选的。那我就所有情况都走一遍呗，比较一下哪种方案用硬币最少就用哪个不就行了么？

最终的算法还真就是基于这个朴实的想法来的。

选第一枚硬币的时候，一共只有三种情况：选择 1，选择 2，选择 5。

  • 如果我们先选了 1，那么再凑出 10 就行了。那怎么凑出 10 呢？不就是 f([1, 2, 5], 10) 么？
  • 如果我们先选了 2，那么再凑出 9 就行了。那怎么凑出 9 呢？不就是 f([1, 2, 5], 9) 么？
  • 如果我们先选了 5，那么再凑出 6 就行了。那怎么凑出 6 呢？不就是 f([1, 2, 5], 6) 么？

上面是选取一个硬币的情况，由于没有凑到 amount，我们继续重复，直到凑到 amount。

于是你可以画出类似如下的逻辑树结构，由于节点太多我没有画全。

有没有发现你的大脑直接处理大问题没有思路，但将其分解为小问题就简单了许多？分完了，我们还要治。

这就好像你是主管，向下面布置了作业，布置完了你还要收作业将他们汇总起来搞个 ppt 啥的。

不过这也不难。由于问题是最少硬币，那么治就取最少呗。

1
1 + min(f([1,2,5], 10),f([1,2,5], 9),f([1,2,5], 6))

总结一下：

这道题的分我们可以从几个特例入手就可以打开思维。上面的分的手段用伪代码描述就是：

1
2
3
for (int coin : coins) {
    f(coins, amount - coin)
}

分完了就是处理边界和治了。

完整的分治代码就是：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public int f(coins, amount) {
    if (amount < 0) {
        // 非法解，用正无穷表示
        return Float.POSITIVE_INFINITY
    }
    // 叶子节点
    if (amount == 0) {
        // 找到一个解，是不是最小的”治“阶段处理。
        return 0
    }
    int ans = Float.POSITIVE_INFINITY
    for (int coin : coins) {
        ans = Math.min(ans, 1 + f(coins, amount - coins))
    }
    return ans
}

为了突出我的算法主框架，略去了一些细节。 比如原题在无解的时候需要返回 - 1，而我返回的是正无穷。

如果之前做过这道题的朋友应该知道这是一个典型的背包问题。如果现在让我做，我可能也直接自底向上 dp table 解决了（不过 dp table 和记忆化递归没有本质的思维差别）。但是算法是如何想出来的这一点，是如何一步一步优化的，大家一定钻到底，这样刷题效率才高。

第三题

不懂题目意思的可以去看下力扣原题 51. N 皇后。这道题就是典型的回溯题目，什么是回溯？一言以蔽之，那就是一个一个试，不行了就返回上一步继续试。

这么多格子我该放哪呢？每个格子还有制约关系！好乱，没有思路。

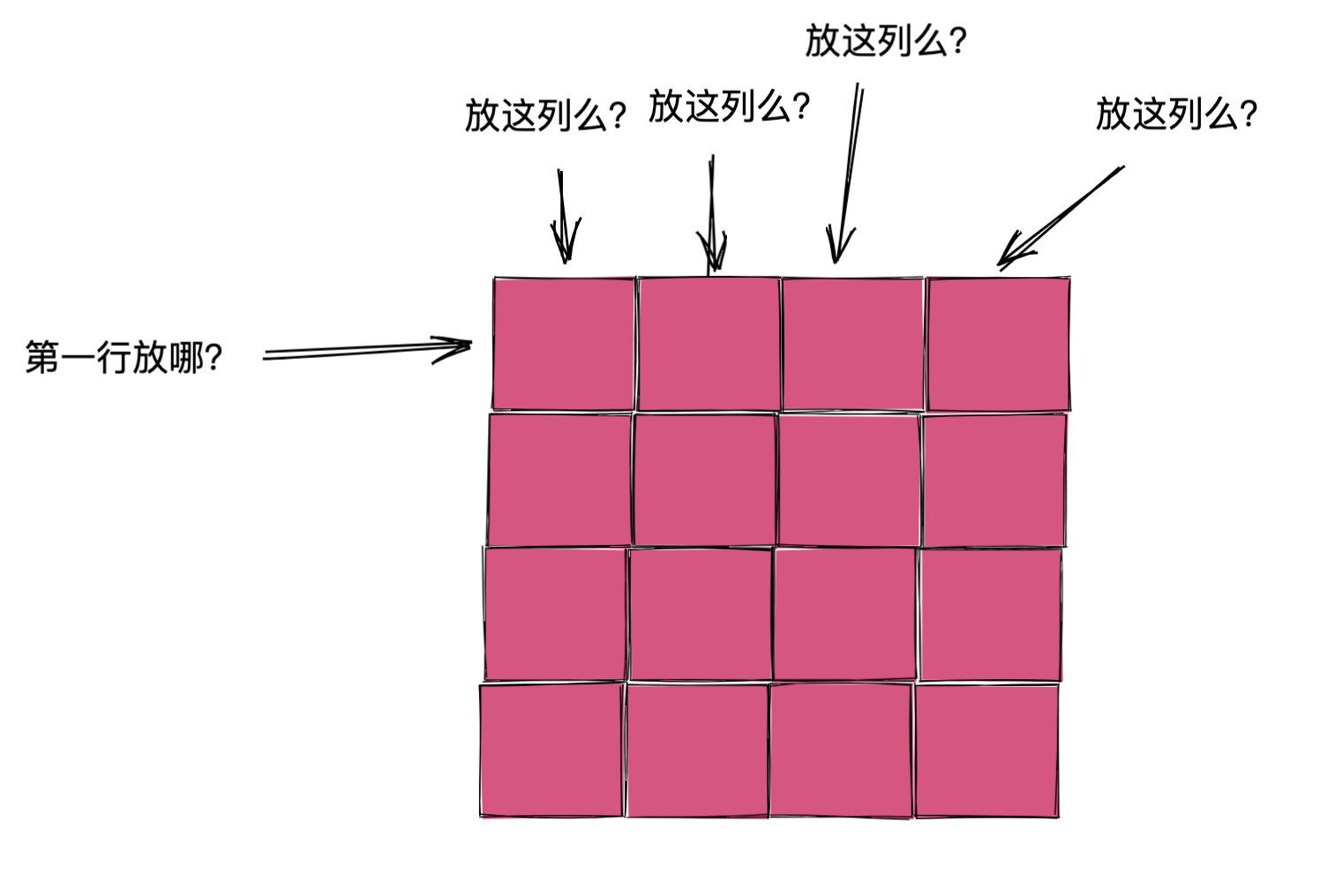
别急，继续使用分治的思维。这道题是让我们将 N 个皇后放到 N X N 的棋盘上。那不就是：

  • 第一行的皇后应该放到第几列？
  • 第二行的皇后应该放到第几列？
  • 第三行的皇后应该放到第几列？
  • 。。。

改成”第 x 列的皇后应该放到第几行？”这种子问题划分模式也是可以的。

伪代码：

1
2
3
4
5
6
7
public int placeRow(i) {
    // 决定应该放到第几列
}

for (int i=0;i<n;i++) {
    placeRow(i)
}

如果上面的子问题都解决了，那整个问题不就解决了么？

但是上面的子问题，还是无法直接解决。比如“第一行的皇后应该放到第几列？”我也不知道啊。没关系，我们继续对“第一行的皇后应该放到第几列？” 这个问题进行分解。

  • 第一行的皇后放到第 1 列么？
  • 第一行的皇后放到第 2 列么？
  • 第一行的皇后放到第 3 列么？
  • 。。。

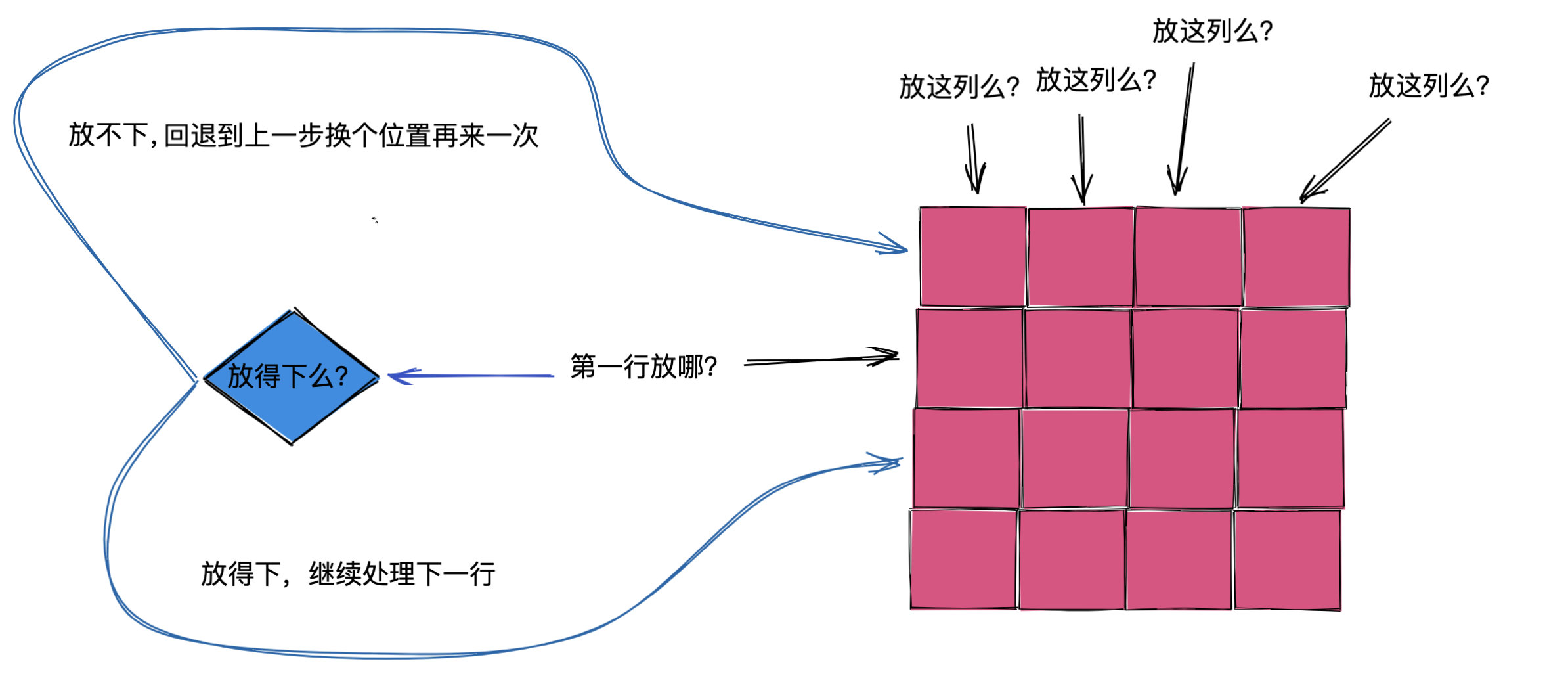
继续完善上面的 placeRow 代码即可。这里给出伪代码：

1
2
3
4
5
6
7
8
9
10
11
public  boolean canPlaceQueue(i, j) {
    // 根据目前的棋局（放了是否能不相互攻击），分析 i 和 j 这个位置能否放女王。
}
public int placeRow(i) {
    for (int j=0;j<n;j++) {
        if (canPlaceQueue(i, j)) {
            // 将女王放到 (i,j)，更新当前棋局
            placeQueue(i, j)
        }
    }
}

现在的问题就只剩下实现canPlaceQueue(i, j) 和 placeQueue(i, j)了，这两个函数根据题目要求模拟实现即可。

需要注意的是我们做了一个placeQueue(i, j) 的操作，这可能是一个 mutable 的操作。因此如果一条路行不通需要回溯，那么 mutable 的数据需要撤销修改。当然如果你的数据是 immutable 就无所谓了。不过 immutable 则有可能内存移除或者超时的风险。

由于这里只是讲思维的，不是讲题目本身的，因此还是点到为止，后面的算法细节我就不讲了，希望读者能自己将代码完善一下。

更多

类似的例子实在太多了，根本举不过来，我随口给大家说几个。

  • 如果让你求一个数组的连续子数组总个数，你会如何求？其中连续指的是数组的索引连续。 比如 [1,3,4]，其连续子数组有：[1], [3], [4], [1,3], [3,4] , [1,3,4]，你需要返回 6。分治就好了，连续子数组个数等于：以索引为 0 结尾的子数组个数 + 以索引为 1 结尾的子数组个数 + … + 以索引为 n - 1 结尾的子数组个数

  • 70. 爬楼梯 让你求爬到最后一级台阶有多少种方法。这太多了，我数不过来。但是我可以将其分解成两个子问题。如果我用 f(n) 表示爬到第 n 级的方法数，那么 f(n) = f(n - 1) + f(n - 2)。但是 n - 1 我也不会啊，没关系，我们继续分解。这和上面的硬币问题有多大差别么？ 对于这道题，分就是拆成两个子问题，治就是求和。

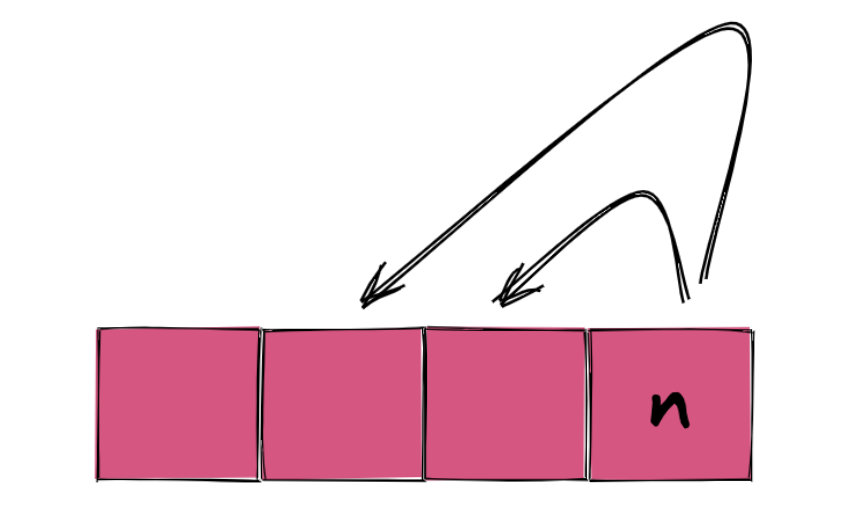
这就是最简单的无选择的递推动态规划

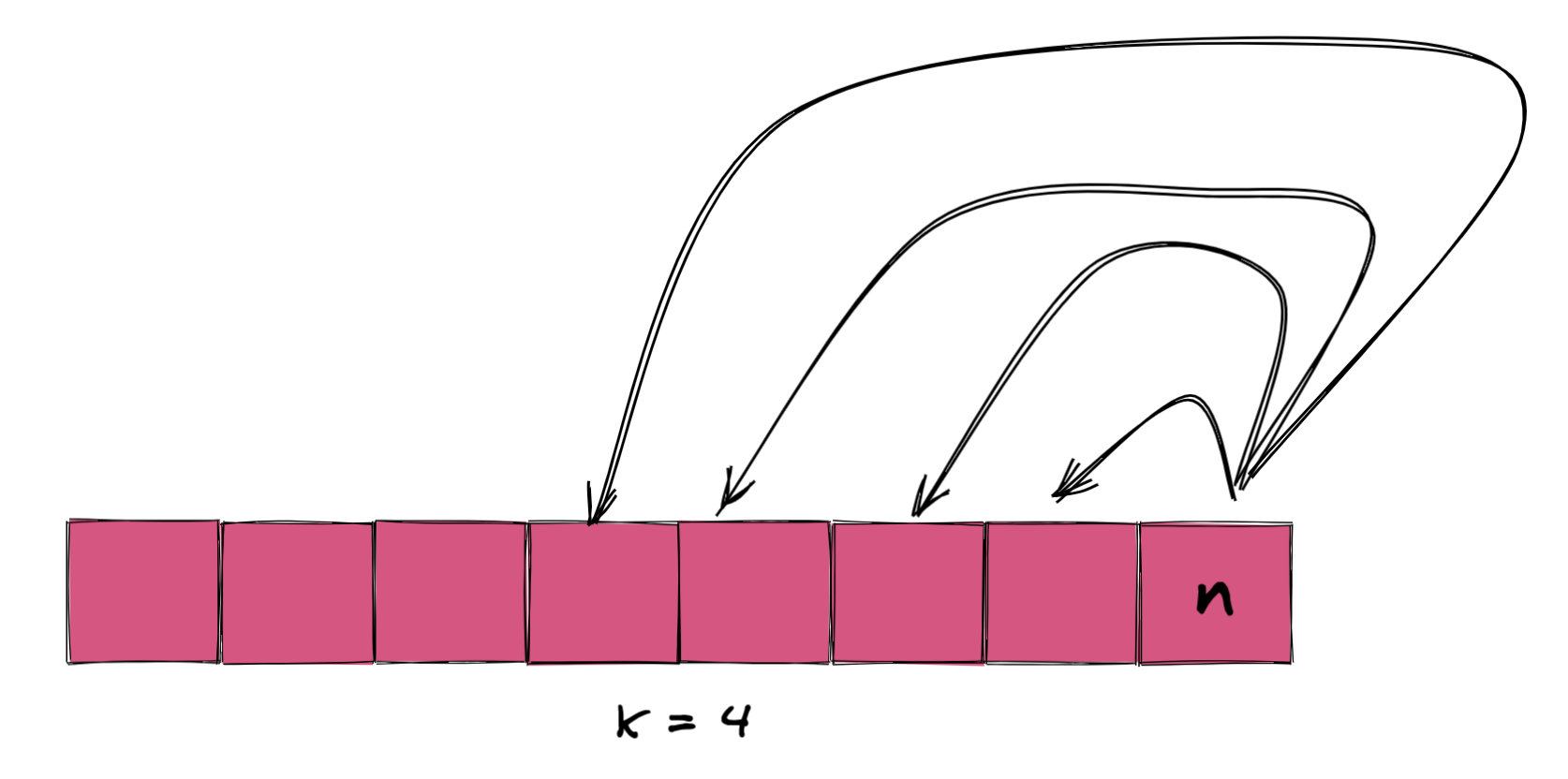
这道题数组长度是 $10^5$，如果不做优化复杂度会是 $N^2$，算起来就是 $10^10$ 过不了，大于上面给大家讲的 1000 万。如何优化有点跑题了，就不在这里讲了。

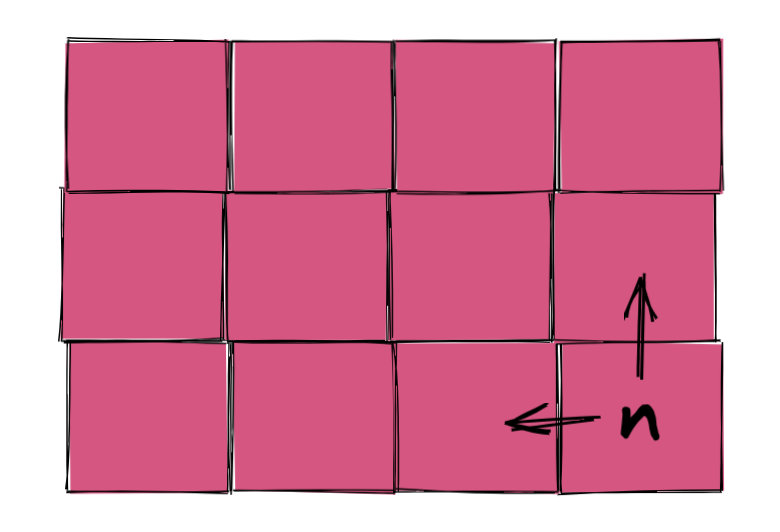
相关换皮题目太多，大家可以去我的插件里看。

总结

本次给大家分享了一个很重要的算法思想分治，很多题都可以用到这个思想。能运用分治思想的专题有“动态规划”,”分治“，“回溯” 等，大家在平时做题的时候可以参考我的这种思考方式。

如果你碰到一个复杂的问题，可以尝试以下几个方法。

  • 不妨先尝试将其拆解，看能否将其拆解成几个小问题。
  • 在草稿上画画图，从特殊情况入手，看能否发现什么蛛丝马迹
  • 暴力模拟。看能否通过剪枝和添加恰当的数据结构来优化算法，使之通过。

如果你有更好的干货技巧，非常希望你能和我交流，万分期待！

除了算法思想，我还和大家分享两个超实用的技巧，分别是：

  • 看关键字。关键字很多时候起到了提示作用，甭管对不对，咱要想到。想到之后迅速脑子中过一下能不能 AC。
  • 看限制条件。 记住一个数字就行了，1000 万。

最后和大家说了一个小心得 - ”不要小看暴力法“。暴力法不仅能帮助你打开思路，有时候甚至暴力 + 剪枝（或数据结构优化）就过了。大力出奇迹，欧耶！(^o^)/

以上就是本文的全部内容了。大家对此有何看法，欢迎给我留言，我有时间都会一一查看回答。更多算法套路可以访问我的 LeetCode 题解仓库：https://github.com/azl397985856/leetcode 。 目前已经 38K star 啦。大家也可以关注我的公众号《力扣加加》带你啃下算法这块硬骨头。


 上一页

LeetCode 堆

 评论


博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本站使用 Material X 作为主题 。
载入天数...载入时分秒...